Живые формы накадэ

Существует три живые формы накадэ из четырех пунктов, которые очень часто применяются на практике. Это –

1. "четыре в линию"
2. " изогнутая четверка"
3. " змейка"

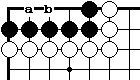Диа.14. Форма накадэ внутри черной группы, называется " четыре в линию". Это живая форма. Она имеет две критические точки "а" и "b". Если белые играют в "а", то черные строят два глаза, играя в "b", и наоборот.

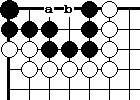Диа.15. Форма накадэ внутри черной группы, называется " изогнутая четверка". Это живая форма. Она имеет две критические точки "а" и "b". Если белые играют в "а", то черные строят два глаза, играя в "b", и наоборот. Хочется отметить, что черным нет необходимости самим играть в "а" или "b", строя два глаза. Этим Вы уменьшите у себя количество очков внутри группы.

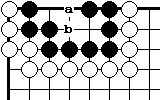Диа.16. Форма накадэ внутри черной группы, называется "изогнутая четверка". Это живая форма. Она также имеет две критические точки "а" и "b".

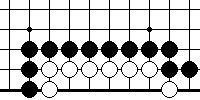Пример 11.

Ход белых

Какой наиболее выгодный способ выживания у белых?

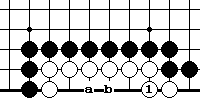Решение примера 11.

Выгодней всего белым выжить, играя 1 и получая форму накадэ "четыре в линию". Это приносит им 4 очка территории. Группа живет, потому что у нее две критические точки "а" и "b". Если выживать ходом в "а", то у белых останется только 3 очка территории.

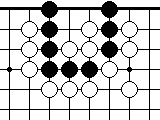Пример 12.

Ход черных

Как им выжить?

Решение примера 1 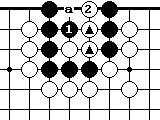2.

Черные должны сыграть 1. Если белые ответят 2, черные снимут их в "а". Тогда накадэ внутри черной группы будет иметь форму "изогнутая четверка". Эта группа живет, потому что имеет две критические точки в пунктах .

Пример 1 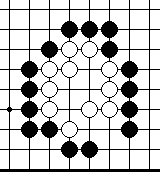3.

Ход белых

Как им выжить?

Решение примера 1 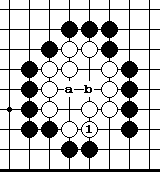3.

Белые должны сыграть 1, образуя форму накадэ " змейка". Теперь белая группа живет, потому что у нее есть две критические точки. Любые другие попытки выжить хуже из-за того, что белые получают меньше территории.

И так, подведем итоги.

Накадэ из 3-х точек имеет только две мертвые формы - "три в линию" и "треугольник".

Накадэ из 4-х точек имеет две мертвые формы – " квадрат" и " пирамида" и три живые формы – " четыре в линию", "изогнутая четверка" и "змейка".

Накадэ из 5-и точек имеет две мертвые формы – " автомобиль" и "звездочка". Все остальные формы накадэ из 5-и точек будут живые. Они, либо строят глаза, либо живут в сэки.

Накадэ из 6-и точек имеет одну мертвую форму – "жук". Все остальные формы накадэ из 6-и точек будут живые. Они, либо строят глаза, либо живут в сэки.

Формы накадэ более 6-и точек всегда живут. Они, либо строят глаза, либо живут в сэки, кроме особых случаев.

Рассмотрим несколько примеров.

Пример 14.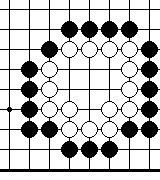

Ход черных.

Могут ли черные убить белых?

Решение примера 14.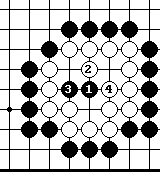

Пространство внутри белой группы состоит из 7-и точек. Значит, она умереть не может. Если черные играют в критическую точку 1, то после варианта 1-4 белые строят два глаза.

Пример 15.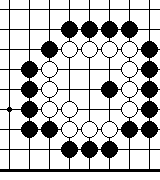

Ход черных.

Могут ли черные убить белую группу.

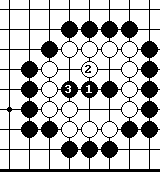
Решение примера 15.

Пространство внутри белой группы состоит из 8-и точек. Значит, она умереть не может. Если черные играют в критическую точку 1, белые ответят в 2, угрожая построить два глаза. Черные играют 3 и в результате получается сэки.

Дата добавления: 2014-11-08; просмотров: 418; Нарушение авторских прав

Мы поможем в написании ваших работ!