Временные характеристики. Операционный метод. Передаточная функция

Временные характеристики

Дифференциальное уравнение является самой общей формой описания элемента и не дает наглядного представления о его передаточных свойствах. Наглядное представление об этих свойствах дает решение дифференциального уравнения. Но одно и то же дифференциальное уравнение может иметь множество решений, конкретный вид которых зависит от начального состояния элемента и вида внешнего воздействия. Поэтому динамические свойства элементов и систем принято характеризовать решением, соответствующим нулевым начальным условиям и одному из типовых воздействий. В качестве типового воздействия принимают единичное ступенчатое воздействие, дельта-функцию или гармоническое воздействие.

Наиболее наглядное представление о динамических свойствах элемента дает его переходнаяфункция или же, как говорят переходная характеристика.

Переходная функция h(t) – это изменение выходной величины у(t) во времени, возникающее после подачи на вход единичного ступенчатого воздействия, при нулевых начальных условиях.

Переходная функция может быть задана в виде графика или в формульном виде.

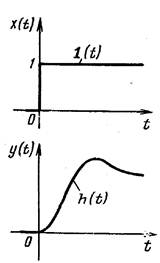
Формульное выражение функции h(t) для конкретного элемента можно найти, решая его дифференциальное уравнение при условиях

1). x(t)=1(t);

2). у(-0)=у⁽¹⁾(-0)=…=y^(n-1)(-0)=0.

Второе условие означает, что выходная величина у и ее производные до (n-1)-го порядка непосредственно перед подачей ступенчатого воздействия равны нулю.

Переходная функция h(t), как и любое решение неоднородного дифференциального уравнения

a₀(dⁿy(t)/dtⁿ)+a₁(d^n-1y(t)/dt^n-1)+…+a_ny(t)=

=b₀(d^mx(t)/dt^m)+b₁(d^m-1x(t)/dt^m-1)+…+b_mx(t)

имеет две составляющие: вынужденную h_В(t) и свободную h_С(t).

Вынужденная составляющая h_В(t) переходного процессапредставляет собой частное решение исходного уравнения. При ступенчатом воздействии вынужденная составляющая равна установившемуся значению выходной величины y, которое для статических элементов может быть определено непосредственно из дифференциального уравнения (при нулевых производных)

h_В(t)=y(∞)=b_m/a_n.

Свободная составляющая h_С(t) находится как решение соответствующего однородного дифференциального уравнения в следующем виде (при отсутствии одинаковых корней)

h_C(t)= ∑С_ke^{λ t},

где λ_k – корни характеристического уравнения;

C_k – постоянные интегрирования, зависящие от начальных условий.

Характеристическое уравнение,соответствующее определенному дифференциальному уравнению, представляет собой, как известно, алгебраическое уравнение, степень и коэффициенты которого совпадают с порядком и коэффициентами левой части этого дифференциального уравнения. Для дифференциального уравнения

a₀dⁿy(t)/dtⁿ+a₁d^n-1y(t)/dt^n-1+…+a_ny(t)=

=b₀d^mx(t)/dt^m+b₁d^m-1x(t)/dt^m-1+…+b_mx(t),

характеристическое уравнение будет иметь вид

a₀λⁿ+a₁λ^n-1+…+a_n=0.

Структура характеристического уравнения совпадает со структурой левой части дифференциального уравнения, записанного в символической форме, и со структурой собственного (характеристического) оператора D(p). Поэтому при записи характеристического уравнения часто вместо символа λ, обозначающего неизвестную переменную алгебраического уравнения, используют символ р. Но при этом р означает уже не операцию дифференцирования, а некоторое комплексное число, которое является корнем характеристического уравнения.

Для линейных элементов и систем, кроме принципа суперпозиции, справедливо еще одно общее правило.

Реакция выходной величины у(t) на неединичное ступенчатое воздействие а₀1(t) равна произведению переходной функции h(t) на величину множителя а₀, т. е. у(t)=a₀h(t).

Это свойство широко используется при исследовании и расчете линейных систем.

Импульсная переходная функция ω(t) – это изменение выходной величины у(t), возникающее после подачи на вход дельта-функции, при нулевых начальных условиях.

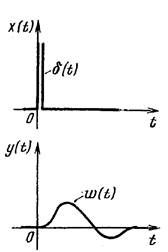
Если входное воздействие представляет собой неединичный импульс a₀δ(t), то ординаты функции выходной величины у(t) будут в a₀ раз больше ординат функции ω(t), т. е. у(t)=a₀ω(t).

Импульсная переходная функция ω(t) равна производной от переходной функции h(t)

ω(t)=dh(t)/dt,

и наоборот, переходная функция h(t) равна интегралу от импульсной переходнойфункции ω(t)

h(t)= ω(θ)dθ.

При помощи импульсной переходной функции элемента можно определить его реакцию на входное воздействие произвольного вида. Связь между изменениями входной и выходной величин во времени устанавливается интегралом свертки

y(t)= x(θ)ω(t-θ)dθ= x(t-θ)ω(θ)dθ.

Данное интегральное соотношение вытекает из следующих рассуждений.

Любое входное воздействие х(t) можно рассматривать как непрерывную последовательность коротких импульсов х(θ)dθδ(t-θ), имеющих площадь х(θ)dθ и действующих в моменты t=θ, где 0<θ<∞. Так как смещенная дельта-функция δ(t-θ), действующая на входе элемента, создает на его выходе смещенную импульсную переходную функцию ω(t-θ), то каждому неединичному входному импульсу х(θ)dθδ(θ-т) на выходе будет соответствовать реакция, пропорциональная импульсной функции, т. е. реакция dy=х(θ)ω(t-т)dθ. Полный переходный процесс на выходе согласно принципу суперпозиции получается в результате суммирования реакций на все входные импульсы, т. е. как результат их интегрирования по аргументу θ от 0 до ∞.

Данное обоснование интеграла свертки объясняет второе распространенное название функции ω(t) – весовая. Действительно, эта функция определяет вес (долю), с которым каждый входной импульс, полученный при разложении сигнала х(t), участвует в формировании результирующего выходного сигнала у(t).

Так как следствие не может опережать причину, действует условие физической осуществимости

при t<0 весовая функция ω(t)Ξ0

при θ>t весовая функция ω(t-θ)Ξ0.

С учетом этого верхний предел интегрирования в интеграле свертки может быть уменьшен до t.

Переходные характеристики h(t) и ω(t) называют также временными.

Дата добавления: 2014-11-14; просмотров: 517; Нарушение авторских прав

Мы поможем в написании ваших работ!