
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
ОПРЕДЕЛЕНИЕ СРЕДНЕЙ ИЗОБАРНОЙ ТЕПЛОЕМКОСТИ ВОЗДУХА
Задание
1. Экспериментальным путем определить массовую среднюю изобарную теплоемкость воздуха.
2. Полученное значение теплоемкости сравнить со справочным, найти расхождение в процентах и проанализировать причины погрешности опытов.
3. По данным п.1 вычислить мольную и объемную изобарные, а также мольную, массовую и объемную изохорные теплоемкости воздуха.
Основные теоретические положения
Понятие теплоемкости используется при определении количества теплоты, участвующего в термодинамическом процессе. Теплоемкостью называется отношение количества теплоты δQ, подведенного к рабочему телу в некотором термодинамическом процессе, к соответствующему изменению температуры dT этого тела.
Если изменение температуры бесконечно малая величина dt, то говорят об истинной теплоемкости:
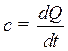 (3.1)
(3.1)
Если же изменение температуры рабочего тела имеет вполне конкретное значение Δt = t2 - t1, то теплоемкость называется средней
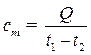 (3.2)
(3.2)
Связь между истинной и средней теплоемкостями может быть установлена из следующего соотношения:
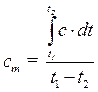 (3.3)
(3.3)
Обычно теплоемкость относят к единице измерения количества вещества, тогда она называется удельной. В соответствии с выбранной количественной единицей различают:
- удельную массовую теплоемкость с, отнесенную к 1 кг газа, Дж/(кг·К);
- удельную объемную теплоемкость с', отнесенную к количеству газа, содержащегося в 1 м3 объема при нормальных физических условиях, Дж/(нм3·К);
- удельную мольную теплоемкость μс, отнесенную к 1 кмоль вещества, Дж/(кмоль·К).
Связь между перечисленными теплоемкостями устанавливается простыми соотношениями:
c = μс /μ; с' = с · ρн; с' = μс /22,4 (3.4)
Учитывая, что 1 м3 при разных параметрах состояния (t; Р) содержит неодинаковую массу газа, для измерения количества вещества используется кубометр, отнесенный к нормальным физическим условиям: Р = 101325 Па (760 мм рт.ст.); Т = 273,15 К (t = 0,1 °С). По той же причине плотность ρн и объем υ = 22,4 м3 одного кмоля газа, в формулах (3.4) соответствуют нормальным условиям.
Для идеального газа теплоемкость зависит от рода газа, характера термодинамического процесса и температуры, а для реальных газов и от давления. То есть – теплоемкость является функцией процесса. Это означает, что одно и то же рабочее тело в зависимости от процесса требует для своего нагревания на 1 К различного количества теплоты. Численно величина теплоемкости (с) может изменяться в пределах от + ∞ до - ∞.
В термодинамических расчетах особую роль играют теплоемкости при постоянном давлении cp и при постоянном объеме cυ. Из уравнений первого закона термодинамики, составленных для условий изобарного и изохорного процессов, легко установить связь этих теплоемкостей с такими важными характеристиками газов, как внутренняя энергия и энтальпия:
- теплоемкость при постоянном давлении (изобарная теплоемкость)
ср = (дh / дt)p, (3.5)
ср = δqр / dT, (3.6)
равная отношению количества теплоты δqp, сообщенной телу в процессе при постоянном давлении, к изменению температуры тела dT;
- теплоемкость при постоянном объеме (изохорная теплоемкость)
сυ = (дu / дt)υ, (3.7)
сυ = δqυ / dT, (3.8)
равная отношению количества теплоты δqυ,подведенной к телу в процессе при постоянном объеме, к изменению температуры тела dT.
Поскольку при изобарном подводе теплоты одновременно с повышением температуры газа увеличивается и его объем, то для нагревания, например, 1 кг газа на 1 К при постоянном давлении необходимо затратить теплоты больше, чем для такого же нагревания при постоянном объеме. Следовательно, ср больше сυ на величину работы, совершенной газом против внешних сил при увеличении его температуры на 1 К в изобарном процессе. Для идеальных газов справедливо соотношение:
сp = сυ + R, (3.9)
Это соотношение называется уравнением Майера и является одним из основных в технической термодинамике идеальных газов. Отметим, что для реальных газов cp - cυ > R, поскольку при их расширении дополнительно затрачивается работа на преодоление сил притяжения между молекулами реального газа.
Выражение (3.9) показывает связь между изобарной и изохорной теплоемкостями газов. Связь между ср и сυ для газов может быть выражена, и через коэффициент Пуассона – показателя адиабаты:
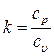 , (3.10)
, (3.10)
Теплоемкости адиабатного и изотермического процессов можно определить, проанализировав формулу (3.1). В случае изотермического процесса dt = 0 и сТ = ∞. В случае адиабатного процесса, когда отсутствует передача тепла dq = 0 и сk = 0.
Теплоемкость политропных процессов в значительной степени зависит от показателя политропы и определяется формулой:
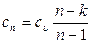 , (3.11)
, (3.11)
где k = cp/cv – показатель адиабаты;
n – показатель политропы;
Обычно теплоемкости определяются экспериментально. Учитывая простоту эксперимента в условиях атмосферного давления, обычно находят изобарную теплоемкость ср , а сv вычисляют по уравнению (3.9).
В эксперименте измеряют количество теплоты Q, подведенное к известному количеству газа G при постоянном давлении, и соответствующее приращение температуры t2 – t1. После чего средняя массовая теплоемкость рассчитывается по формуле:
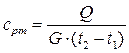 , (3.12)
, (3.12)
Для практических расчетов теплоемкости всех веществ, сводят в таблицы, причем с целью сокращения объема таблиц средние теплоемкости приводят в них для интервала температур от 0 до t (таблица теплоемкостей приведена в приложении II). Наряду с табличной формой теплоемкость в справочнике может быть представлена формулами вида:
c = a + bt , (3.13)
Массовая теплоемкость газовых смесей, если смесь задана в массовых долях, рассчитывается по формуле:
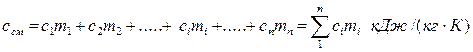 (3.14)
(3.14)
Описания экспериментальной установки
Схема экспериментальной установки показана на рисунке 3.1. Суть экспериментального определения изобарной массовой теплоемкости ср состоит в следующем. Воздух вентилятором 1 прокачивается через стеклянную теплоизолированную трубку 2 и воспринимает теплоту от электронагревателя 3, помещенного внутри нее. При этом температура воздуха увеличивается на величину Δt, которая измеряется хромель-копелевой термопарой 4 и цифровым прибором – Щ301 5 работающим как милливольтметр. Холодный и горячий спай термопары расположены соответственно до и после экспериментального участка. Расход нагреваемого воздуха измеряется с помощью ротаметра 6, установленного на входе в экспериментальный участок. Ротаметр представляет собой прозрачную трубку с внутренним коническим расширяющимся кверху каналом, внутри которого свободно движется поплавок. Поток воздуха, проходя через кольцевой зазор между поплавком и трубкой, дросселируется. Возникающий при этом перепад давлений поддерживает поплавок во взвешенном состоянии на высоте, пропорциональной расходу. Таким образом, имея тарировочную кривую или аналитическую зависимость V = ƒ(h), no высоте подъема поплавка h определяют объемный расход V.
 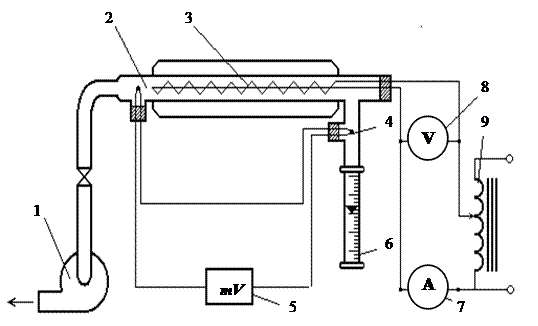 |
Рисунок 3.1 – Экспериментальная установка для измерения температур:
1 – вентилятор; 2 – теплоизолированная трубка; 3 – электронагреватель; 4 – термопара подсоединенная к милливольтметру; 5 – милливольтметр; 6 – ротаметр; 7 – амперметр; 8 – вольтметр; 9 – автотрансформатор.
Необходимые для определения плотности воздуха на входе в экспериментальный участок давление и температура измеряются барометром и жидкостным термометром. Количество воспринимаемого воздухом тепла при установившемся режиме равно мощности электронагревателя, которая измеряется амперметром 7 и вольтметром 8 и задается ЛАТРом 9. Чтобы можно было приравнять мощность нагревателя и количество тепла, полученное воздухом, необходимо тщательно теплоизолировать экспериментальный участок, исключив тем самым потери тепла в окружающее пространство. Роль тепловой изоляции выполняет оболочка, в которой создан вакуум, а внутренняя поверхность посеребрена.
Порядок выполнения работы
Включается вентилятор и в зависимости от типа привода частотой вращения (двигатель постоянного тока) или заслонкой на воздухопроводе (двигатель переменного тока) устанавливается такой расход воздуха, чтобы поплавок ротаметра находился между 3 и 4 делениями.
Тумблером (26 В) включается питание цифровых вольтметра и амперметра. ЛАТРом устанавливается напряжение примерно 60 В, при этом ток в нагревателе не превышает 0,5 А.
После выхода установки на стационарный тепловой режим, о чем свидетельствует неменяющееся в течение 5 минут значение термоЭДС, показания приборов записываются в таблицу наблюдений. Затем, изменив расход воздуха ориентировочно на 1 деление ротаметра, опыт повторяется в той же последовательности.
Таблица наблюдений
| Величина | Размерность | Значения в опытах | |||
| Наименование | Обозначение | ||||
| Показания ротаметра | h | дел. | |||
| Расход воздуха | V | м3/час | |||
| Давление воздуха перед ротаметром | P0 | мм рт.ст. | |||
| Температура воздуха перед ротаметром | t1 | ° С | |||
| Падение напряжения на электронагревателе | U | В | |||
| Ток в электронагревателе | I | А | |||
| Приращение температуры воздуха в экспериментальном участке | Е | мВ |
После завершения работы сначала отключается нагреватель. И только убедившись, что температура на выходе из экспериментального участка снизилась до комнатной (термоЭДС близка к нулю), можно выключить вентилятор.
Обработка экспериментальных данных
1. По показаниям амперметра и вольтметра рассчитывается мощность нагревателя, кВт, которая при стационарном режиме равна теплоте, полученной воздухом:
Q = U·I·10-3
2. Плотность воздуха перед ротаметром определяется по уравнению Менделеева – Клапейрона, кг/м3
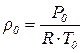
где Р0, Т0 – давление и абсолютная температура воздуха перед ротаметром; R – газовая постоянная (R = 287 Дж/(кг·К)).
3. Часовой объемный расход воздуха, м3/час вычисляется по формуле
V = 0,64·h + 0,95
4. Приращение температуры в экспериментальном участке, °С, находится по термоЭДС
Δt = 15·E
5. Средняя изобарная теплоемкость воздуха равна:
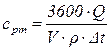 , кДж/(кг·К)
, кДж/(кг·К)
6. Справочное значение теплоемкости воздуха, кДж/(кг·К), рассчитывается по уравнению
сpmспр = 0,996 + 0,93·10-4 (t1 + t2),
где температура в конце процесса (на выходе из экспериментальной установки) t2 = t1 + Δt.
7. Погрешность опыта составляет
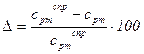
8. Мольная изобарная теплоемкость, кДж/(кмоль·K)
μсp = cp·μ = cp·29
9. Объемная изобарная теплоемкость, кДж/(нм3·К)
c'p = μсp /22,4
10. Массовая изохорная теплоемкость, кДж/(кг·К)
сυ = ср – R = ср – 0,287
11. Мольная изохорная теплоемкость, кДж/(кмоль·К)
μсυ = cυ·μ = cυ·29
12. Объемная изохорная теплоемкость, кДж/(нм3·К)
c'υ = μсυ /22,4
Контрольные вопросы и задания
Для допуска к лабораторной работе.
1. Что является целью работы?
2. Из каких элементов состоит экспериментальная установка?
3. В какой последовательности включаются элементы установки? (Порядок выполнения работы).
4. Что такое установившийся режим? Его признак.
5. Каким образом в работе определяется расход воздуха?
6. Когда производится запись показаний приборов?
7. Какой метод используется для определения теплоемкости?
Дополнительные вопросы для защиты работы.
8. Дайте определение теплоемкости.
9. Что такое истинная и средняя теплоемкости?
10. Напишите связь между истинной и средней теплоемкостями?
11. Что называется удельной теплоемкостью вещества? Перечислите удельные теплоемкости, укажите единицы их измерения и связь между ними?
12. Почему объемная теплоемкость отнесена к нм3, а не просто к м3?
13. От чего зависит теплоемкость идеального и реального газов?
14. Какая из двух теплоемкостей ср или сυ больше и почему (объясните, используя выражение 1-го закона термодинамики)?
15. Чему равна теплоемкость изотермического и адиабатного процессов?
16. Может ли теплоемкость быть отрицательной?
17. Как, пользуясь понятием теплоемкости, вычислить количество тепла? Для всех ли процессов можно это сделать?
18. В каком случае истинная и средняя теплоемкости численно равны?
| <== предыдущая страница | | | следующая страница ==> |
| Описания экспериментальной установки | | | МАТЕРИАЛЫ К ЛЕКЦИЯМ |
Дата добавления: 2014-11-14; просмотров: 2106; Нарушение авторских прав

Мы поможем в написании ваших работ!