Упражнения по решению задач

2.1 Демодуляция и декодирование сигнала при
передаче в канале с постоянными параметрами

Пример 1. Мощность сигнала на входе демодулятора равна Р_с=10^–12 Вт, а скорость передачи составляет V=20 МБод. Спектральная плотность мощности белого шума N_o=10^–20 Вт·с.

Определить битовую вероятность ошибки при демодуляции:

а) двоичного сигнала с ФМ в когерентной СПИ;

б) двоичного сигнала с ОФМ в частично-когерентной СПИ;

а) ортогональных сигналов с ЧМ в когерентной СПИ.

Решение. а) Энергия одного импульса в сигнале с ФМ, ОФМ или ЧМ не зависит от значения переданного символа и равна Тогда отношение сигнал/шум равно Из формулы (5.14) [2] имеем , и битовая вероятность ошибки из формулы (5.13) [2] равна

б) Из формулы (5.19) [2] получаем

в) Из формулы (5.18) [2] имеем

Пример 2. В условиях примера 1б система фазовой автоподстройки частоты генератора несущей в приемнике вносит постоянную ошибку γ=30^о. Определить битовую вероятность ошибки при демодуляции.

Решение. Если начальная фаза опорного колебания w(t) на выходе системы ФАПЧ (рис. 5.6 [2]), подаваемого на корреляционный приемник, отличается от начальной фазы входного сигнала φ_с при передаче символа 0, это не изменяет характеристик шумовой составляющей v_ш напряжения на его выходе, но уменьшает величину его сигнальной части v_с, которая при условии ω_о(t_к–t_н) >> 1 приближенно равна

Как и следовало ожидать, эта величина максимальна при нулевой расстройке γ = 0. То же происходит и при передаче импульса противоположной полярности.

Таким образом, эквивалентное отношение сигнал/шум q² уменьшается в раза, то есть на 1,25 дБ.

Пример 3. Во сколько раз нужно увеличить мощность сигнала для обеспечения той же вероятности ошибки приема на фоне белого шума, если при ФМ вместо традиционных значений начальной фазы импульсов 0^о и 180^о использовать значения 0^о и 60^о ?

Решение. ФМ может применяться только в когерентной СПИ. Вероятность ошибки при демодуляции двоичного сигнала зависит только от отношения энергии разностного сигнала к спектральной плотности шума. Для классической ФМ амплитуда разностного сигнала равна удвоенной амплитуде импульса. При ФМ значений начальной фазы импульсов 0^о и 60^о амплитуда разностного сигнала равна амплитуде импульса, то есть в два раза меньше. Тогда для обеспечения той же вероятности ошибки нужно увеличить мощность сигнала в четыре раза.

Пример 4. Напряжение v на выходе интегратора корреляционного приемника в когерентной СПИ с двоичной ФМ распределено по нормальному закону с параметрами:

m_v = m₀ = 5, σ_v = 2, если передан символ 0;

m_v = m₁ = –5, σ_v = 2, если передан символ 1.

Символы 0 и 1 передаются одинаково часто. Определить:

а) значение порога v_п, обеспечивающее минимум полной вероятности ошибки р_а, и вычислить величину р_а;

б) вероятности ошибок первого и второго рода α_б и β_б, а также полную вероятность ошибки р_б в случае, когда v_п = 1,5;

в) вероятности ошибок первого и второго рода α_в и β_в, полную вероятность ошибки р_в, а также вероятность стирания символа р_с в случае, когда применяется мягкая процедура вынесения решения, а значения порогов установлены v_п1 = –1 и v_п2 = 1.

Решение. а) Из формулы (5.10) [2] имеем для вероятности ошибки первого рода , а из формулы (5.11) [2] для вероятности ошибки второго рода . В итоге, учитывая равновероятность символов 0 и 1, имеем для полной вероятности ошибки по формуле (5.12) [2]

.

Чтобы найти значение порога v_п, обеспечивающее минимум полной вероятности ошибки, дифференцируем это выражение по переменной v_п и приравниваем производную к нулю. Получим уравнение

, решением которого является значение v_п = 0 (рис. 5.1 [2]). Тогда величина р_а вычисляется по формуле (5.13) [2]

б) когда v_п = 1,5, из формул (5.10) – (5.12) [2] получаем

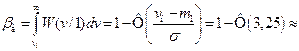
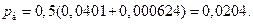
Итак, полная вероятность ошибки оказалась больше.

в) Из рис. 5.12 [2] видно, что

р = 0,00135,

а вероятность стирания символа

Пример 5. Определить, во сколько раз увеличится битовая вероятность ошибки на выходе демодулятора в когерентной СПИ, если для шестикратного увеличения битовой скорости передачи вместо двоичной ФМ применить КАМ при том же отношении сигнал/шум на входе демодулятора в 20 дБ.

Решение. Отношение сигнал/шум по энергии равно

В системе с ФМ из формулы (5.12) [2] и табл. 5.1 [2] имеем и

Для шестикратного увеличения скорости нужно использовать КАМ–64, для которой из табл. 5.1 [2] имеем

Затем из формулы (5.16) [2] находим вероятность ошибки при демодуляции импульса, то есть шестибитовой комбинации

Нумерацию 64 позиций сигнала с КАМ–64 можно задать так, что соседние шестибитовые комбинации будут отличаться не более чем в двух битах. Тогда битовая вероятность ошибки будет равна В итоге при переходе от ФМ к КАМ–64 битовая вероятность ошибки возрастет примерно на 20 порядков.

Пример 6. В некогерентной двоичной СПИ с ортогональными сигналами не применяется помехоустойчивое кодирование, при этом отношение сигнал/шум на входе демодулятора составляет 10 дБ. Определить, удастся ли без увеличения мощности передатчика уменьшить битовую вероятность ошибки, если использовать 31-разрядный код БЧХ, способный исправлять все однократные и двукратные ошибки.

Решение. Отношение сигнал/шум по энергии равно

По формуле (5.18) [2] находим для битовой вероятности ошибки без помехоустойчивого кодирования

Из Приложения 1 [1] получаем значения параметров заданного кода БЧХ: всего в комбинации 31 символ, из них информационных только 21 символ. Тогда при передаче длительность символа придется уменьшить в 31/21 раз, поэтому отношение сигнал/шум по энергии будет равно

Далее аналогично находим новое значение для битовой вероятности ошибки на выходе демодулятора

Вероятность ошибки при декодировании кодовой комбинации определим по формуле (3.59) [1]

Кодовое расстояние используемого кода равно 5 (см. соотношение (3.6) [1]), тогда по формуле (3.60) [1] находим значение битовой вероятности ошибки на выходе декодера

Итак, использование кода БЧХ позволило уменьшить битовую вероятность ошибки на выходе СПИ в 1,37 раза.

Пример 7. В цифровой СПИ применяется мягкая процедура демодуляции в соответствии с условиями примера 4в и используется код Хэмминга (7,4) для восстановления стертых символов. Определить битовую вероятность ошибки на выходе декодера.

Решение. В условиях примера 4в вероятность того, что символ не окажется стертым и будет принят безошибочно, равна

Восстановление стертых символов производится в предположении, что остальные символы комбинации на входе декодера ошибок не содержат. Стертым символам нужно присвоить такие значения, которые удовлетворяют всем r=3 проверкам на четность, задаваемым тремя строками проверочной матрицы этого кода (3.27) [1]

Например, в принятой комбинации S₁0S₃1010 стертые символы S₁ и S₃ участвуют во второй и третьей проверках, то есть в разрешенной комбинации должно быть (напомним, что суммирование проводится по модулю 2)

0 + S₃ + 1 + 0 = 0, S₁ + S₃ + 0 + 0 = 0.

Отсюда имеем S₁ = S₃=1. Очевидно, что код способен восстановить любые один или два стертых символа (например, три символа S₁, S₂ и S₃ не могут быть восстановлены, так как они участвуют всего в двух проверках).

Таким образом, кодовая комбинация будет декодирована правильно в любой из четырех несовместных ситуаций:

1) в комбинации нет стертых и ошибочных символов;

2) в комбинации один символ стерт, остальные без ошибок;

3) в комбинации два символа стерты, остальные без ошибок;

4) в комбинации нет стертых символов, но один символ с ошибкой.

Вероятность каждого из этих событий равна

Вероятность правильного декодирования комбинации вычисляем по формуле сложения вероятностей

Вероятность ошибочного декодирования комбинации

В итоге битовая вероятность ошибки на выходе декодера определяется по формуле (3.60) [1]

2.2 Демодуляция сигнала при передаче в канале
с замираниями (разнесенный прием)

Пример 8. Оценить суммарное время нарушения связи за 1 час работы, если это происходит при снижении уровня сигнала на 12 дБ по сравнению с его средним значением по мощности.

Решение. Среднее значение мощности, то есть квадрата случайной величины А в формуле (5.21) [2], равно

тогда для порогового значения в формуле (5.21) [2] имеем Вероятность того, что амплитуда окажется ниже порога, равна

Тогда в течение 1 часа суммарное время нарушения связи составит приблизительно

Пример 9. Решить пример 8 в предположении, что применяется четырехкратный разнесенный прием с автовыбором максимального сигнала.

Решение. Флуктуации сигналов в ветвях разнесения независимы, поэтому вероятность совместного снижения уровня сигналов во всех ветвях находим по формуле умножения вероятностей

Тогда в течение 1 часа суммарное время нарушения связи составит приблизительно

Пример 10. В канале с релеевскими замираниями применяется N-кратный разнесенный прием при условии, что суммарное среднее по энергии отношение сигнал/шум в ветвях разнесения составляет 20 дБ. Определить битовую вероятность ошибки р для двух случаев:

а) кратность разнесения равна 2;

б) кратность разнесения равна 16.

Каково минимально-возможное значение р?

Решение. Из данных рис. 5.10 [2] получаем для битовой вероятности ошибки значение 10^–3 для случая двукратного разнесения и 10^–7 для 16-кратного. Из того же рисунка видно, что минимально-возможное значение р =3·10^–8 достигается при использовании 32-кратного разнесенного приема.

Дата добавления: 2014-11-14; просмотров: 264; Нарушение авторских прав

Мы поможем в написании ваших работ!