Лекция 5. Средние величины

5.1. Понятие статистической средней.

5.2. Основные условия правильного расчета и применения

средней.

5.3. Основные виды средних.

5.4. Средняя арифметическая и средняя гармоническая.

5.1. Средние величины относятся к третьему этапу статистической методологии – к методу обобщающих статистических показателей. Это один из важнейших методов обобщающих статистических показателей.

Средними в статистике называют показатели, выражающие характерные, типичные размеры общественных явлений по одному признаку. Они необходимы потому, что количественный признак варьирует, колеблется. Если бы не было вариации, не было бы и смысла в вычислении средней.

Вариация признака возникает в связи с различием условий для каждой единицы совокупности. Несмотря на индивидуальные различия, отдельные единицы имеют общее, типичное. Это общее, типичное и проявляется в средней. При осмыслении средней выделяют два момента:

1. что статистическая средняя является характеристикой обязательно конкретных общественных явлений, т.е. учитываются условия места и времени. Эта конкретность условий места и времени отличает среднюю статистическую от средней математической;

2. что средняя является типической характеристикой, она дает характеристику не чего-то случайного, а типичного, поэтому она характеризует объективный уровень признака явления, достигнутый к определенному периоду или моменту времени.

Основное назначение средней в том, чтобы одним числом дать обобщающую цифровую характеристику однокачественному количеству с точки зрения одного признака, величина которого у отдельных единиц совокупности варьирует.

Отличительная особенность средней в том, что характеризуя в целом совокупность, она не характеризует каждую отдельную единицу совокупности. Средняя – своего рода абстракция, но это не лишает ее научного значения, т.к. она отражает типичное, характерное для совокупности.

5.2. Основные условия применения средней относят к тому, чтобы средняя отражала объективный, реальный уровень. Для этого необходимо следующее:

1. расчет следует вести по однородным, однокачественным явлениям. Чтобы рассчитать средние только для качественно однородных групп, необходимо всю совокупность предварительно разгруппировать на такие группы; выделить типы явлений, форм, предприятий и только после этого рассчитывать среднюю. Таким образом, метод средних должен основываться на методе статистических группировок;

2. при анализе общественных явлений общие средние необходимо дополнять групповыми средними и индивидуальными величинами. Сочетание общих средних, групповых средних и индивидуальных величин позволяет выявить не только типичное, характерное, но и прогрессивное, и отсталое;

3. средние показатели необходимо рассчитывать на основе массовых данных, т.е. нужно исчислять средние по всему кругу явлений или по типичной их части. Только тогда средняя будет отражать реальный уровень. При расчете средней необходимо иметь как минимум 20-30 единиц;

4. необходим правильный выбор явления, т.е. единиц совокупности, по которым рассчитывается средняя. Например, для расчета среднего количества кормов для содержания скота необходимо брать за единицу совокупности не дойную, а фуражную корову.

5.3. Для определения среднего показателя применяются различные по способу расчета виды средних. Это средняя арифметическая, средняя гармоническая, средняя квадратическая и средняя геометрическая.

Средние, которые применяются в статистике, относятся к классу степенных средних. Они вычисляются по формуле:

, при m=1 мы получаем формулу средней арифметической;

при m=-1 - формула средней гармонической;

при m=2 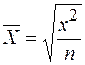- формула средней квадратической;

при m→0 - формула средней геометрической.

Они применяются в экономических и плановых расчетах. Средняя квадратическая применяется при расчете показателей вариации для характеристики степени колеблемости признака, средняя геометрическая – при определении средних темпов роста, прироста и снижения.

Дата добавления: 2014-11-20; просмотров: 210; Нарушение авторских прав

Мы поможем в написании ваших работ!