Задачи стохастического управления

Тема: Аппарат асимптотических представлений дисперсий модальных полиномиальных моделей в задаче проектирования регуляторов при стохастических воздействиях

Задачи стохастического управления

Существует две задачи стохастического управления:

1. – помеха, которая должна порождать на выходе системы составляющую минимальной величины;

2. – полезный сигнал, который должен с минимальной ошибкой быть воспроизведён на выходе системы.

При использовании для проектирования регулятора метода модального управления требуется задать модальную модель желаемого процесса, соответствующего некоторым показателям качества. При задании модальных моделей широкое распространение получили полиномиальные динамические модальные модели (ПДММ), под которыми понимаются модели, матрица состояния которых является сопровождающей матрицей некоторого стандартного полинома .

Наиболее употребляемыми полиномами, используемыми при назначении желаемой динамической модели управляемого процесса, являются полином Баттерворта и бином Ньютона. Коэффициенты этих полиномов параметризованы характеристической частотой , так что . Значение характеристической частоты определяет расположение корней характеристических полиномов ПДММ на комплексной плоскости, а следовательно и показатели качества переходных процессов в системе.

В задачах стохастического управления в качестве показателя качества могут быть заданы требуемые значения дисперсий выхода системы и ошибки . Первой задаче стохастического управления соответствует требование минимизации дисперсии выхода системы, а второй – минимизация дисперсии ошибки. Следовательно, чтобы регулятор для нашей системы обеспечивал выполнение услови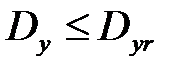й или дисперсии ПДММ должны так же соответствовать этим условиям.

В Лекции 6 приведены аналитические представления относительных дисперсий выхода и ошибки для ПДММ степеней 1-5 с характеристическими полиномами Баттерворта и Ньютона, параметризованные относительной частотой из которых, зная требуемые значения дисперсий , можно вычислить требуемое и получить желаемые ПДММ. Однако, как известно из математики, алгебраическое уравнение с одним неизвестным степени выше 4-й неразрешимо в радикалах, то есть не существует формулы, выражающей корни общего уравнения степени выше 4-й через коэффициенты с помощью операций сложения, вычитания, умножения, деления, возведения в натуральную степень и извлечения корней натуральной степени.

В примечании к Лекции 6 говорится о целесообразности получения асимптотических представлений полученных аналитических представлений дисперсий, что позволило бы найти для ПДММ 5 степени и выше и упростить расчёт для степеней 1-4. Получение асимптотических представлений дисперсий выхода и ошибки осуществляется в силу условий:

1.

2.

Таким образом, для получения асимптотического представления дисперсии выхода нужно оставить члены числителя и знаменателя с минимальными степенями, а для получения асимптотического представления дисперсии ошибки оставить члены числителя и знаменателя с максимальными степенями, а. Рассмотрим подробно получение асимптотических дисперсий на нескольких примерах.

2. Аппарат относительной дисперсии для системы возбуждаемой стохастическим входным воздействием типа "экспоненциально коррелированный окрашенный шум"

Рассмотрим для примера модальную модель второго порядка, заданную уравнением:

где – экспоненциально коррелированный шум, 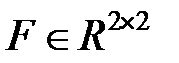– матрица состояния системы, замкнутой единичной отрицательной обратной связью, – матрица входа. Передаточная функция модальной модели задаётся в виде:

Согласно Лекции 4, дисперсии выхода и ошибки данной системы представлены следующими выражениями:

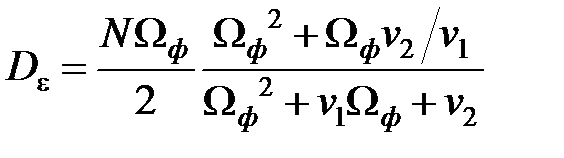
Используя параметризацию коэффициентов характеристической частотой, получаем следующие выражения для передаточной функции:

и дисперсий:

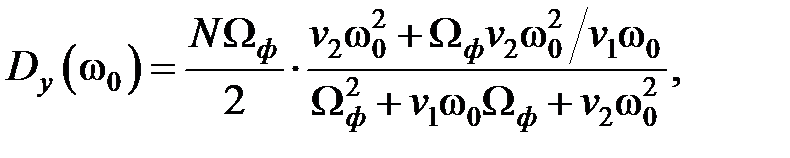
где 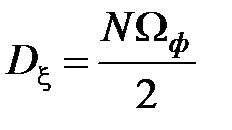– дисперсия выхода формирующего фильтра.

Рисунок 1 – Структурное представление задачи

Получим выражения для относительных дисперсий входа и ошибки в два этапа:

¾ введём замены: тогда выражения для дисперсий примут вид:

¾ введём относительную характеристическую частоту после подстановки которой получаем следующие выражения для относительных дисперсий выхода и ошибки:

Получим выражения асимптотических дисперсий для рассматриваемой системы:

1.

2.

Таким образом, в ходе преобразований при вычислении дисперсий, были выделены доминирующие члены в выражениях дисперсий. Назовём выражения

1.

2.

асимптотическими представлениями дисперсий выхода и ошибки .

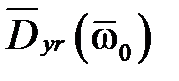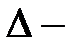Предположим, что , а , причём и являются заданными величинами. Тогда, в случае, если и имеют значения, близкие к 0 (а следовательно для первого случая или для второго, где достаточно малая величина), то асимптотические представления дисперсий выхода и ошибки можно считать некоторым справедливым приближением к ним и использовать эти представления для вычисления с некоторой точностью требуемой характеристической частоты :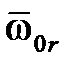

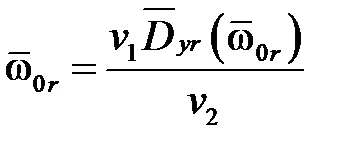(10.1)

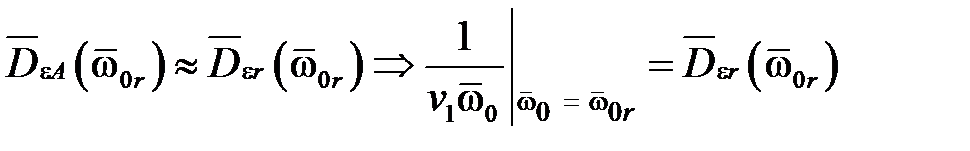
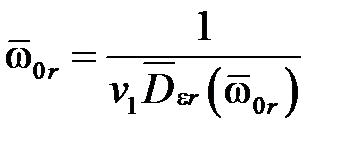(10.2)

3. Аппарат относительной дисперсии для системы возбуждаемой окрашенным шумом типа "нерегулярная качка"

Введём в рассмотрение относительные дисперсии выхода и ошибки модальной модели второго порядка, заданной уравнением:

где – шум типа "нерегулярная качка". Передаточная функция модальной модели задана в виде:

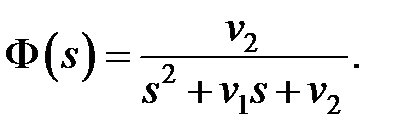
Согласно Лекции 4, дисперсии выхода и ошибки системы представлены следующими выражениями:

Используя параметризацию коэффициентов характеристической частотой получаем следующие выражения для передаточной функции:

и дисперсий:

где 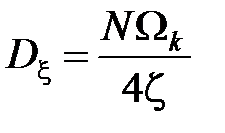– дисперсия выхода формирующего фильтра.

Получим выражения для относительных дисперсий входа и ошибки в два этапа:

¾ введём замены: тогда выражения для дисперсий примут вид:

¾ введём относительную характеристическую частоту после подстановки которой получаем следующие выражения для относительных дисперсий выхода и ошибки:

Получим выражения асимптотических дисперсий для рассматриваемой системы:

1.

2.

Таким образом, в ходе преобразований при вычислении дисперсий, были выделены доминирующие члены в выражениях дисперсий. Назовём выражения

1.

2.

асимптотическими представлениями дисперсий выхода и ошибки .

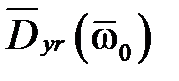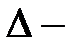Предположим, что , а , причём и являются заданными величинами. Тогда, в случае, если и имеют значения, близкие к 0 (а следовательно для первого случая или для второго, где достаточно малая величина), то асимптотические представления дисперсий выхода и ошибки можно считать некоторым справедливым приближением к ним и использовать эти представления для вычисления с некоторой точностью требуемой характеристической частоты :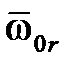

(10.3)

(10.4)

Дата добавления: 2014-11-20; просмотров: 211; Нарушение авторских прав

Мы поможем в написании ваших работ!