Работа лопаточного колеса. Формула Эйлера

Основой частью всякого лопаточного нагнетателя является колесо, которое при вращении передает жидкости (газу) подводимую от двигателя мощность.

В других частях нагнетателя (кожухе, направляющих аппарата) величина полного давления может только уменьшаться, хотя статическое давление растет из-за уменьшения динамического давления.

Чтобы пояснить происходящий в лопаточных колесах процесс передачи мощности двигателя воздуху (это при рассмотрении аэродинамики вентиляторов), т.е. процесс образования давления, развиваемого радиальным вентилятором, рассмотрим вывод уравнения для определения давления.

Рассмотрим движение жидкости (или воздуха) вдоль лопатки вращающегося центробежного колеса. Абсолютную скорость движения С можно по правилу параллерограмма разложить на две составляющие:

1. переносную или окружную скорость, направленную по касательной к данной точке окружности,

U=ωr, [м/с],

где ω – частота вращения, (угловая скорость) [рад/с]

r – радиус, [м].

2. относительную скорость ω, направленную по касательной в данной точке.

Рассмотрим (см. рис.) треугольник этих скоростей непосредственно перед входом на лопатку (с индексом 1) и сразу после выхода с нее (с индексом 2)

а) движение вдоль лопатки.

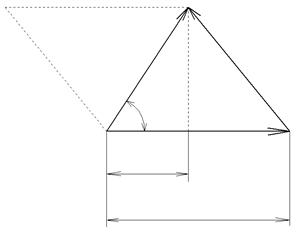
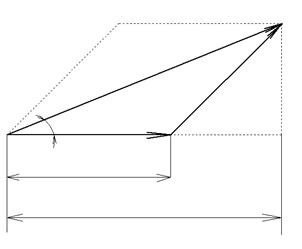
б) при входе на лопатку в) при выходе с лопатки

Рисунок. Векторы скоростей.

Из треугольников скоростей на основе тригонометрических соображений получим:

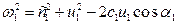
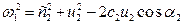
Представим себе движение жидкости (воздуха или газа для вентиляторов) в канале между двумя лопатками колеса без каких-либо потерь. Приращение полного давления (теоретического) будет равняться сумме приращений статического и динамического давлений:

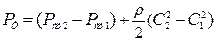
Статическое давление на пути движения в канале будет увеличиваться за счет работы центробежной силы и возможного уменьшения относительной скорости в канале (диффузорного эффекта), т. е. приращение будет равно:

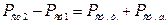
Центробежная сила:

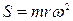
где m – масса жидкости;

r - радиус;

ω - угловая скорость (частота вращения).

Секундная работа этой силы на пути движения воздуха в канале (энергия) выразится уравнением:

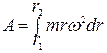
Так как давление представляет собой энергию, отнесенную к единице объема, а масса в единице объема является плотностью m\V=ρ, то

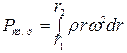
Откуда после интегрирования получим

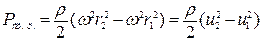
Приращение статического давления за счет изменения относительной скорости при расширении потока в канале (диффузорного эффекта) составит

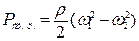
Приращение полного давления получим после суммирования и соответствующего преобразования составляющих

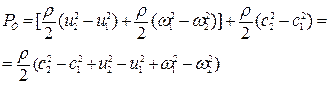
Если значения 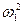и 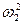заменить выражениями, полученными выше из треугольника скоростей, то после преобразования получим уравнение, определяющее величину теоретического давления, развиваемого лопаточным колесом:

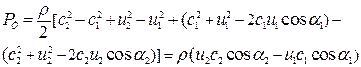
Будет считать скоростью закручивания проекцию абсолютной скорости на направление окружной скорости 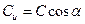(а безразмерным закручиванием – отношение 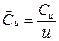или ).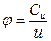

Подставив эти значения, получим уравнение давления

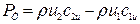I

Отношение скорости закручивания к окружной скорости называется коэффициентом закручивания.

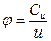откуда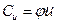

После подстановки значения φ уравнение давления примет вид:

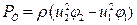II

Уравнения давления (I и II ), развиваемого лопаточным колесом, было выведено еще в 1755 году, Эйлером для бесконечного количества лопаток и равномерного распределения скоростей.

Формула Эйлера лежит лежит в основе расчета всех лопаточных нагнетателей.

В тех случаях, когда к колесу подтекает незакрученный поток, т.е. когда С_1u=0, очевидно, что φ₁=0 и формула (II) примет вид:

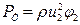III

Формулы I-III дают значение давления, развиваемого лопастным колесом при отсутствии потерь. В действительности при движении жидкости в нагревателе происходят различные потери, которые учитываются коэффициентом полезного действия, характеризующим отношение полезной (теоретической) мощности N_т к мощности затраченной:

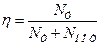
Где N_пот – теряемая мощность

Обозначив 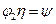, где величина ψ носит название коэффициента давления, получим

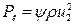
Где P_к – действительное давление, развиваемое колесом с учетом потерь.

Таким образом, давление, создаваемое лопастным колесом, равно произведению коэффициента давления на массовую плотность перемещаемой жидкости (или газа) и на квадрат окружной скорости на внешней (выходной) кромке лопатки.

Если выражение P_к является упрощенным видом формулы Эйлера для лопастного колеса, работающего в условиях подтекания незакрученного потока жидкости или газа (так называемый безударный вход потока).

Коэффициент давления ψ.

Коэффициент давления ψ зависит от коэффициента закручивания φ₂ ( 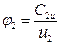) т.е. зависит от формы профиля лопаток.

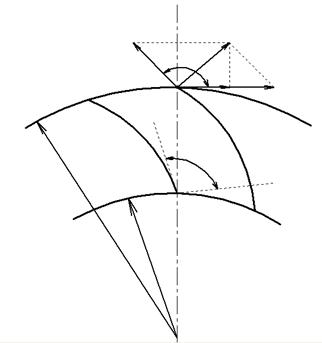
В зависимости от положения выходной кромки лопатки могут быть загнутыми

а) назад при β₂> 90⁰

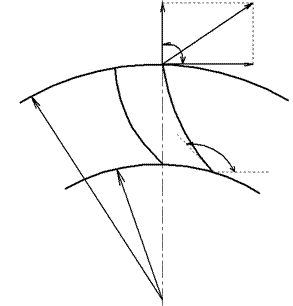
б) радиальными при β₂ =90⁰

в) загнутыми вперед при β₂< 90⁰

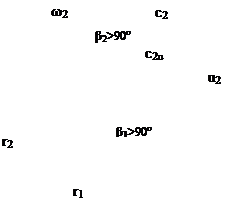
а) б)

Ψ=0,4-0,7 Ψ=0,7-0,9

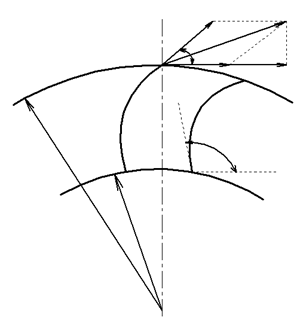
в)

Ψ=0,8-1,3; 1,5

Дата добавления: 2014-11-20; просмотров: 397; Нарушение авторских прав

Мы поможем в написании ваших работ!