Компактность, теорема Левенгейма-Сколема, теорема об общем элементарном расширении

Зафиксируем язык 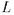, соответствующий сигнатуре 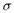; мы собираемся снаб­дить множество 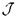всех полных теорий в языке 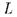топологией: любому пред­ложению 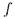этого языка поставим в соответствие множество 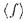всех полных теорий, содержащих 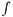; таким образом 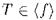означает 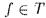или ещё 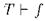(читается " 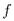следствие 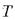" или ещё " 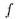выводимо из 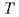"; чтобы не злоупо­треблять символом 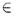, мы остановимся на последнем обозначении). Так как 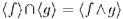множества 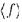образуют базу топологии, которой мы снабжа­ем 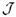. Множество 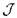с этой топологией образует сепарабельное пространство; на самом деле, если 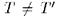, поскольку 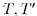- полные теории, то для некоторого предложения 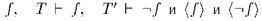- непересекающиеся окрестности соответственно .

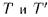Так как дополнением для 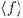будет 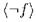, открытые множества из базы будут одновременно закрытыми: 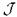есть так называемое вполне несвязное про­странство (пространство, допускающее базу открыто-замкнутых множеств); как следствие каждое непустое связное подмножество 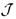состоит из одной точ­ки.

Итак, по определению, открытое подмножество 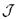является объединением множеств вида 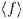, а замкнутое - пересечением таковых. Непустые замкнутые подмножества 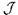соответствуют в точности неполным теориям в языке 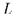: если 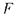- пересечение множеств 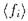, то ему ставится в соответствие теория 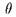, аксиоматизируемая предложениями 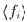; 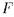есть в точности множество полных теорий, содержащих 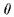(заметим, что 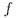выводимо из каждая полная теория, содержащая 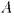, содержит ).

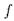Следующая теорема компактности является одной из самых существенных для теории моделей; всё было сделано для того, чтобы обеспечить финитный характер формул, который обеспечивает её законность.

Теорема 4.4 (компактности ) Пространство 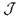полных теорий в языке 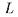является вполне несвязным компактом.

Доказательство. Мы уже показали, что 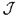сепарабельно и вполне несвяз­но. Остается показать, что любой ультрафильтр над 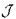сходится, т.е. являет­ся утончением фильтра окрестностей некоторой точки. Для каждой 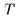из 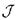выберем модель 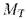для 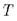, и пусть 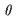- теория модели 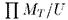; если 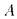- окрестность 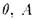содержит некоторое множество такое, что 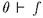, то по теореме Лося 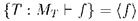принадлежит , так же как и .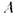

Вполне несвязный компакт часто называют стоуновским или простран­ством Стоуна это - самое естественное обобщение понятия конечного про­странства с дискретной топологией. Другая, формулировка теоремы 4.4 - следующая :

Теорема 4.5 (компактности ) Для совместности бесконечного множества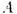

формул достаточна совместность каждой конечной части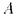

Теорема 4.6 1) Если 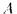- противоречивое множество формул, то существу­ет конечная противоречивая часть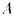

2) Если 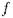- следствие 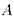, то существует конечная часть 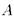, из которой следует .

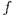Доказательство. 1) эквивалентно предыдущему утверждению; чтобы до­казать 2), заметим, что 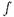- следствие 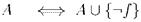противоречиво.

Можно сказать, что теорема компактности находит постоянное применение в теории моделей; здесь мы начнем с поразительных примеров этого применения.

Теорема 4.7 Открыто-замкнутыми подмножествами 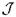являются множе­ства вида 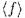. где 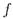- предложение, и только они.

Следствие теоремы компактности : если 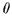конечно аксиомати­зируема, то из любой аксиоматизации 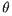можно выделить конечную аксиома­тизацию .

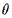Теорема 4.10 (Левенгейм — Сколем) Если 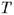-теория, не обязательно пол­ная, имеющая бесконечную модель или сколь угодно большие конечные модели, тогда 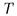имеет модель мощности 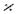для любого кардинала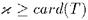

Рассмотрим теперь модель M полной теории T в языке L. Пусть L(M) -язык, полученный добавлением к L константного символа для каждого элемен­та M , и пусть T(M) - множество предложений, истинных в этом новом языке. Принадлежность 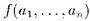к T(M) , где 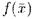- формула языка L означает что 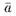из M удовлетворяет 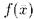, т.е. что 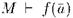; T(M) называется диаграммой M. Некоторые называют диаграммой M множество бескванторных предложений L(M) истинных в M, его мы назовём "свободной диаграммой" M . Мы видим, что по определению элементарное расширение M есть не что иное, как модель T(M) и также, что из теоремы Левенгейма-Сколема следует, что если M бесконечна, то она имеет элементарное расширение мощности 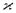для любого кардинала 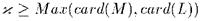. Все это показывает, что элементарная эквивалентность может характери­зовать с точностью до изоморфизма только конечные структуры; например, счетная структура счетного языка имеет элементарное расширение в любой бесконечной мощности.

Лемма 4.11 Если M и N - две элементарно эквивалентные структуры, то они имеют общее элементарное расширение : существует структура P и элементарные вложения MuNвP.

Лемма 4.12 Если M и N элементарно эквивалентны, то M элементарно вкладывается в некоторую ультрастепень N .

На самом деле, верен намного более сильный результат : если две струк­туры M и N элементарно эквивалентны, то существует ультрафильтр U, такой, что 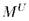и 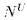изоморфны. Но вот это - трудная теорема, последний этап доказательства которой потребовал вмешательство Шелаха ; она требует глубоких знаний в теории моделей и об ультрафильтрах. Впрочем, она почти не применяется специалистами в теории моделей : можно было бы, разумеет­ся, наличие изоморфных ультрастепеней принять за определение элементарной эквивалентности.

Эта теорема Шелаха отвечает на проблему нахождения "алгебраической" характеризации (т.е. не использующей логику, формулы, выполнимость, по­нятия, происхождение которых может показаться подозрительным для опре­деленных математиков) элементарной эквивалентности. На совершенно ином и значительно более простом уровне локальные изоморфизмы вместе с рангом Фраиссе дают один такой ответ. Но ответ Фраиссе, в отличие от ответа Шела­ха, снабжает эффективным и непосредственным методом доказательства того, что две структуры элементарно эквивалентны.

Теорема 4.14 Если М_i семейство элементарно эквивалентных структур, то они имеют общее элементарное расширение : существует структура M и элементарные вложения 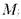в M для каждого i .

Доказательство. Итерируя лемму 4.11 , доказываем теорему, если се­мейство структур Mi конечно. Если оно бесконечно, то теорема компактности сводит вопрос о совместности 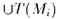, где множество имен элементов предполагается дизъюнктным, к конечному случаю.

Дата добавления: 2014-11-24; просмотров: 426; Нарушение авторских прав

Мы поможем в написании ваших работ!