
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Тема 4. Системы счисления, используемые в ЭВМ
Позиционные и непозиционные системы счисления. Перевод чисел из любой системы счисления в десятичную. Перевод чисел из десятичной системы счисления в любую. Системы счисления, используемые в ЭВМ (с основанием 2n). Арифметические действия в различных системах счисления
Система счисления – это принятый способ записи чисел и сопоставления этим записям реальных значений. Разнообразные системы счисления, которые существовали раньше и которые используются в наше время, можно разделить на два класса: непозиционные и позиционные.
В непозиционных системах счисления от положения цифры в записи числа не зависит величина, которую она обозначает. Наиболее известным примером непозиционной системы счисления является римская система (римские цифры). В римской системе в качестве цифр используются латинские буквы:
I(1) V(5) X(10) L(50) C(100) D(500) M(1000)
В римских числах цифры записываются слева направо в порядке убывания. В таком случае их значения складываются. Если же слева записана меньшая цифра, а справа – большая, то их значения вычитаются.
Примеры: III(три), VI(четыре),LIX(пятьдесят девять), DXV(пятьсот пятнадцать)
В позиционных системах счисления величина, обозначаемая цифрой (знаком) в записи числа, зависит от ее позиции. Количество используемых цифр (знаков) называется основанием позиционной системы счисления. За основание системы можно принять любое натуральное число — два, три, четыре и т.д.
Система счисления, применяемая в современной математике, является позиционной десятичной системой. Ее основание равно десяти, т.к. запись любых чисел производится с помощью десяти цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Позиционный характер этой системы легко понять на примере любого многозначного числа.
Например, в числе 333 первая тройка означает три сотни, вторая – три десятка, третья – три единицы. Для записи чисел в позиционной системе с основанием n нужно иметь алфавит из n цифр. Обычно для этого при n < 10 используют n первых арабских цифр, а при n > 10 к десяти арабским цифрам добавляют буквы. Вот примеры алфавитов некоторых систем:
| Основание | Система счисления | Алфавит |
| Двоичная | 0 1 | |
| Троичная | 0 1 2 | |
| Четверичная | 0 1 2 3 | |
| Пятеричная | 0 1 2 3 4 | |
| Восьмеричная | 0 1 2 3 4 5 6 7 | |
| Десятичная | 0 1 2 3 4 5 6 7 8 9 | |
| Шестнадцатеричная | 0 1 2 3 4 5 6 7 8 9 A B C D E F |
Если требуется указать основание системы, к которой относится число, то оно приписывается нижним индексом к этому числу. Запись чисел в каждой из систем счисления с основанием q означает сокращенную запись выражения
Aq=±(an-1qn-1+ an-2qn-2+...+ a0q0+ a-1q-1+ a-2q-2+ a-mq-m),
здесь А – само число, q – основание системы счисления, аi – цифры (знаки) данной системы счисления, n – число разрядов целой части числа, m – число разрядов дробной части числа.
Примеры (индекс внизу указывает основание системы счисления):
37,2510 =3*101+7*100+2*10-1+5*10-2,
325,78=3*82+2*81+5*80+7*8-1,
А5,F16=10*161+5*160+15*16-1.
При работе с компьютерами приходится параллельно использовать несколько позиционных систем счисления, поэтому большое практическое значение имеют процедуры перевода чисел из одной системы в другую. Способ перевода чисел из любой позиционной системы счисления в десятичную продемонстрирован в приведенных выше примерах.
Для перевода десятичных чисел в другие системы счислениянеобходимо:
Перевод целых чисел.
1) Основание новой системы счисления выразить в десятичной системе счисления и все последующие действия производить в десятичной системе счисления;
2) последовательно выполнять деление данного числа и получаемых неполных частных на основание новой системы счисления до тех пор, пока не получим неполное частное, меньшее делителя;
3) полученные остатки, являющиеся цифрами числа в новой системе счисления, привести в соответствие с алфавитом новой системы счисления;
4) составить число в новой системе счисления, записывая его, начиная с последнего частного.
Перевод дробных чисел.
1) Основание новой системы счисления выразить в десятичной системе и все последующие действия производить в десятичной системе счисления;
2) последовательно умножать данное число и получаемые дробные части произведений на основание новой системы до тех пор, пока дробная часть произведения не станет равной нулю или не будет достигнута требуемая точность представления числа в новой системе счисления;
3) полученные целые части произведений, являющиеся цифрами числа в новой системе счисления, привести в соответствие с алфавитом новой системы счисления;
4) составить дробную часть числа в новой системе счисления, начиная с целой части первого произведения.
Перевод смешанных чисел, содержащих целую и дробную части, осуществляется в два этапа. Целая и дробная части исходного числа переводятся отдельно по соответствующим алгоритмам. В итоговой записи числа в новой системе счисления целая часть отделяется от дробной запятой (точкой).
Для перевода чисел из 2-ной в 8-ную и наоборот, из 2-ной в 16-ную и наоборот, из 8-ной в 16-ную и наоборот, используется таблица следующего вида:
| Основание системы | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | - | ||
| - | - | ||
| 10 (А) | - | - | |
| 11 (В) | - | - | |
| 12 (С) | - | - | |
| 13 (D) | - | - | |
| 14 (E) | - | - | |
| 15 (F) | - | - |
При переводе в 8-ную систему или из нее необходимо группировать в тройки биты, а при переводе в 16-ную или из нее – группировать их в четверки битов.
Примеры.

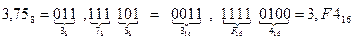
Вопросы для самоконтроля
1. Что такое система счисления? Каковы основные атрибуты системы счисления?
2. Как переводятся целые числа из десятичной системы счисления в другую систему? Привести примеры.
3. Как переводятся дробные числа из десятичной системы счисления в другую систему? Привести примеры.
4. Какая система называется позиционной (непозиционной)?
5. Объясните переводы чисел из одной системы в другую по схемам:
2↔8, 8↔2, 2↔16, 16↔2, 8↔16, 16↔8,
Дата добавления: 2014-11-24; просмотров: 1084; Нарушение авторских прав

Мы поможем в написании ваших работ!