Аппарат относительной дисперсии

Используем рассмотренную параметризацию для решения задачи стохастического управления. Целью стохастического управления является минимизация дисперсии выхода системы, в случае, если входное воздействие является помехой, или минимизация дисперсии ошибки, в случае, если входное воздействие – полезный сигнал.

Введём в рассмотрение относительные дисперсии выхода и ошибки модальной модели. Для примера, рассмотрим модальную модель второго порядка, заданную уравнением:

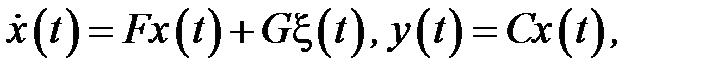
где 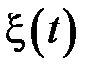– экспоненциально коррелированный шум. Передаточная функция модальной модели задана в виде:

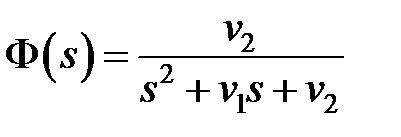
Согласно Лекции 4, дисперсии выхода и ошибки системы представлены следующими выражениями:

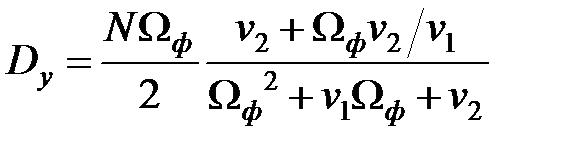
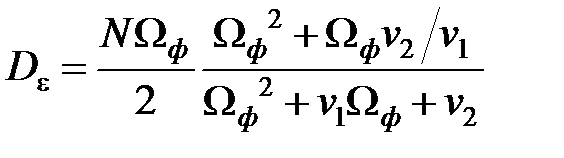
Используя параметризацию коэффициентов, получаем следующие выражения для передаточной функции:

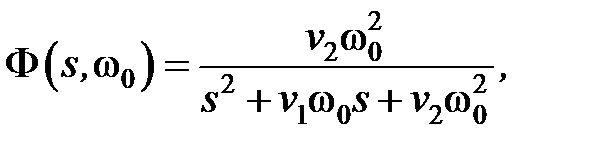
и дисперсий:

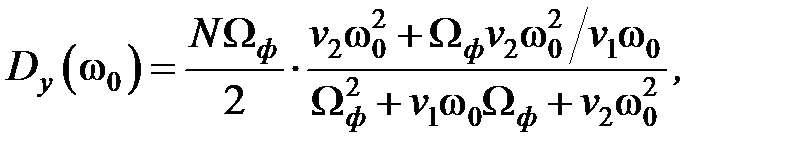
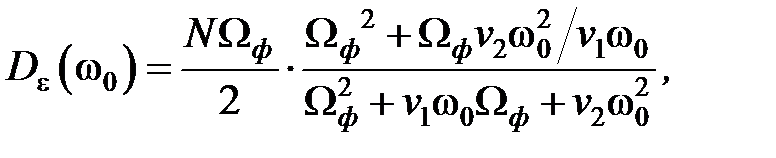
где – дисперсия выхода формирующего фильтра, 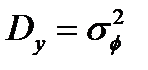, 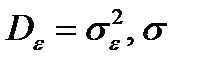– среднеквадратичное отклонение.

Рисунок 9.2 – Структурное представление задачи

Будем решать задачу получения относительных дисперсий входа и ошибки в два этапа:

¾ введём замены: 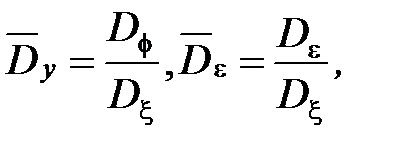тогда выражения для дисперсий примут вид:

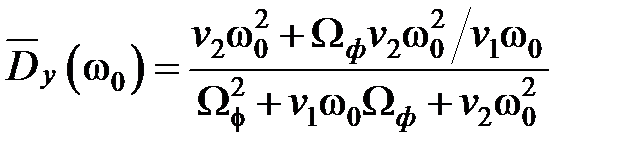
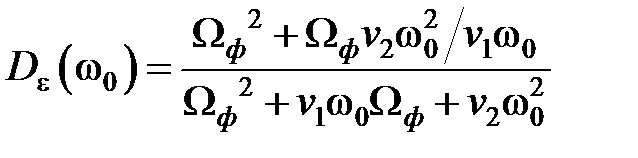
¾ введём относительную характеристическую частоту 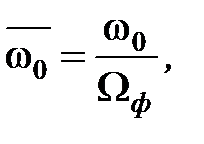после подстановки которой получаем следующие выражения для относительных дисперсий выхода и ошибки:

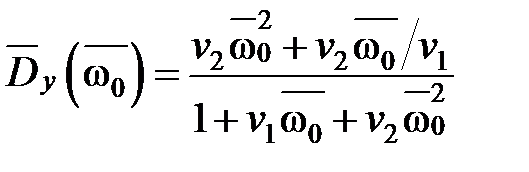
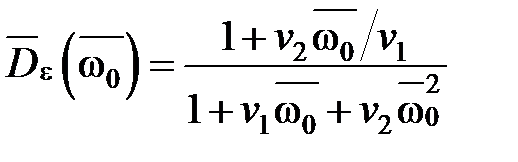
Существует две задачи стохастического управления:

1.

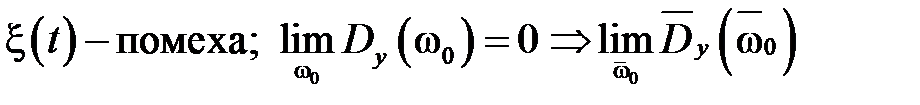
2.

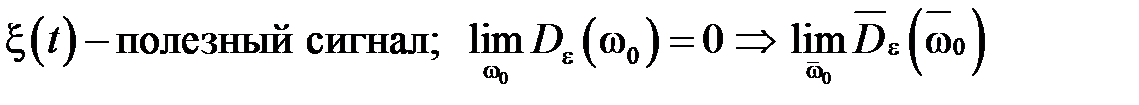
При решении задачи минимизации дисперсии выхода или ошибки, проектируемой системы, на основе приведенных аналитических представлений относительных дисперсий выхода и ошибки целесообразно построить их асимптотические формы. Для этого в случае минимизации дисперсии ошибки нужно оставить члены числителя и знаменателя с максимальными степенями, а для получения асимптотического представления дисперсии выхода нужно оставить члены числителя и знаменателя с минимальными степенями.

Получим выражения асимптотических дисперсий для рассматриваемой системы:

1.

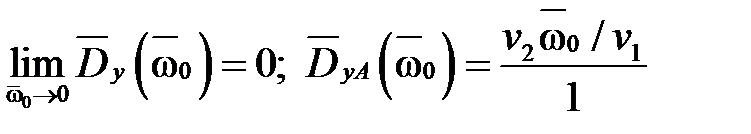
2.

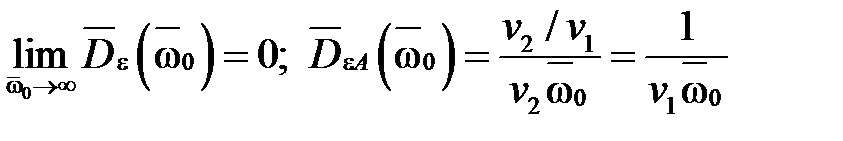
Задача синтеза полиномиальной динамической модальной модели (ПДММ) желаемых процессов для систем со стохастическим входным воздействием типа "экспоненциально коррелированный шум" может быть решена с помощью следующих алгоритмов.

Дата добавления: 2014-11-24; просмотров: 302; Нарушение авторских прав

Мы поможем в написании ваших работ!