
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
НЕЛИНЕЙНЫЕ УРАВНЕНИЯ И СИСТЕМЫ УРАВНЕНИЯ
Лабораторная работа № 1
Распад разрыва в механике сплошной среды
Введение
Многие современные задачи механики сплошных сред связаны с изучением возникновения и распространения различных разрывных течений. На разрывах должны выполнятся три основных закона сохранения: массы, количества движения и энергии. К ним как правило, добавляют дополнительные соотношения, которые следуют либо из экспериментальных исследований, либо являются обобщением большого числа натурных наблюдений. В ряде случаев оказывается, что решения справа и слева от поверхности разрыва однородны, то есть значения газо-динамических величин не зависят ни от временной переменной, ни от пространственных координат. С течением времени изменяются только размеры этих областей, но не значения временных переменных в них. Это свойство оказывается справедливым в течении некоторого временного интервала.
При этих условиях появляется возможность сформулировать математическую задачу, представляющую собой систему нелинейных уравнений, решая которую можно определить скорость распространения разрывов, а следовательно, и размеры соответствующих областей.
Рассмотрим несколько таких случаев.
I.1. Распад разрыва с уравнением состояния идеального газа
Одним из важных условий правильного описания поведения разрывного решения я-я выполнение основных законов сохранения на поверхности разрыва. Получим полезные соотношения для дальнейших преобразований.
Для простоты остановимся на одномерном пространственном варианте и будем рассматривать задачу в неподвижной декартовой системе координат, которой назовем лабораторной.
Пусть справа от разрыва давление в среде 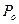 , массовая скорость
, массовая скорость 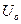 , а слева – давление
, а слева – давление 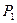 , массовая скорость
, массовая скорость 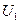 . Предположим, что сам разрыв перемещается по пространству в лабораторной системе координат со скоростью
. Предположим, что сам разрыв перемещается по пространству в лабораторной системе координат со скоростью 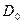 . В этом случае законы сохранения массы и импульса на разрыве могут быть записаны в следующем виде:
. В этом случае законы сохранения массы и импульса на разрыве могут быть записаны в следующем виде:
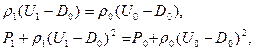 (1)
(1)
где 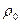 и
и 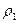 - это значения плотности справа и слева от поверхности разрыва.
- это значения плотности справа и слева от поверхности разрыва.
Выражая 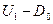 из уравнения (1), подставляя во второе уравнение и разрешая относительно
из уравнения (1), подставляя во второе уравнение и разрешая относительно 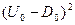 , получаем
, получаем
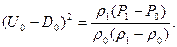 (3)
(3)
Совершенно аналогично находим, что
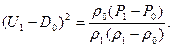 (4)
(4)
Вычтем из (4) почленно (3) и преобразуем полученное выражение:
 (5)
(5)
Выразим 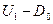 через
через 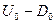 из (1) и подставим в (5):
из (1) и подставим в (5):
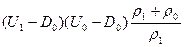 , имеем
, имеем
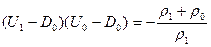 (6)
(6)
Извлечем квадратный корень из левой и правой части (3), исключим 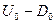 из (6) и разрешим относительно
из (6) и разрешим относительно 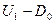 :
:
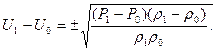 (7)
(7)
При выводе соотношения (7) были использованы законы сохранения массы и импульса. Добавим к ним закон сохранения энергии:
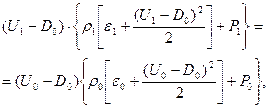 (8)
(8)
предварительно преобразовав его, где через 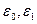 обозначены удельные внутренние энергии справа и слева от точки разрыва. Так как по предположению газ идеальный, то удельная внутренняя энергия, плотность, давление и показатель адиабаты связаны соотношением
обозначены удельные внутренние энергии справа и слева от точки разрыва. Так как по предположению газ идеальный, то удельная внутренняя энергия, плотность, давление и показатель адиабаты связаны соотношением
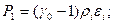 i=0,1. (9)
i=0,1. (9)
Вынесем из фигурных скобок в уравнении (8) справа - 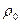 , а слева -
, а слева - 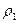 . Затем почленно поделим на (1):
. Затем почленно поделим на (1):
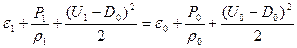 (10)
(10)
Найдем 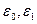 из (9) и подставим в (10):
из (9) и подставим в (10):
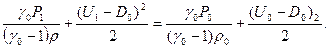 (11)
(11)
Выразим отношение плотностей по разные стороны от разрыва через отношение давлений. Для этого подставим (3) и (4) в (11):
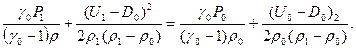
После умножения правой и левой части этого равенства на разность и произведение плотностей, приведения подобных членов приходим к выражению
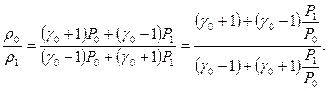 (12)
(12)
Найдем теперь отношение 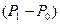 /
/ 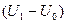 , поделив
, поделив 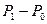 на (7):
на (7):
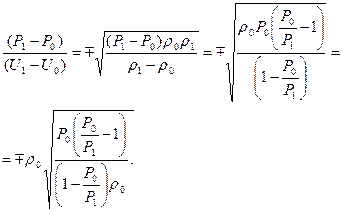 (13)
(13)
Скорость звука в газе связана с плотностью и давлением выражением 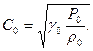
Подставим 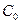 и отношение плотностей из (12) в правую часть в (13). В результате имеем
и отношение плотностей из (12) в правую часть в (13). В результате имеем

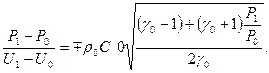 (14)
(14)
Допустим что справа от разрыва значения плотности 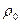 , скорости
, скорости 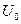 , давления
, давления 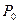 , а также показатель адиабаты
, а также показатель адиабаты 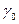 нам известны, а нужно определить значения слева от разрыва, имеющие индекс 1 и скорость движения фронта разрыва
нам известны, а нужно определить значения слева от разрыва, имеющие индекс 1 и скорость движения фронта разрыва 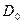 . Соотношения (1)-(14) позволяют это сделать, если дополнительно известно одно из искомых неизвестных
. Соотношения (1)-(14) позволяют это сделать, если дополнительно известно одно из искомых неизвестных 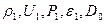 или какая то комбинация из них.
или какая то комбинация из них.
Известны четыре основных варианта распада разрыва [1]:
1)с образованием 2х ударных волн;
2)с ударной волной и волной разряжения;
3)с 2мя волнами разряжения;
4)с 2мя центрированными волнами разряжения.
Остановимся более подробно на первых двух.
I.1.1 Распад разрыва с возникновением двух ударных волн
Пусть в начальный момент все пространство можно разделить на два однородных полупространства, граница между которыми проходит по плоскости разрыва. Для определенности будем считать, что газодинамические величины справа от этой плоскости имеют индекс 0, а слева индекс 3.
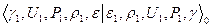
Со временем в результате распада разрыва по правому и левому полупространствам начинают распространятся две ударные волны. Припишем индекс 1 газодинамическим параметрам за правой ударной волной и индекс 2 за левой.
Контактный
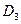 разрыв
разрыв 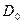
|
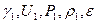 |
| 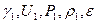
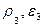 |
| 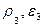
|
Запишем три основных закона сохранения массы, количества движении и энергии на левой и правой ударных волнах и условия непрерывности давления и массовой скорости на контактном разрыве:
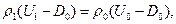
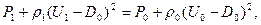
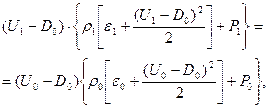
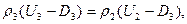 (15)
(15)
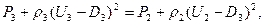
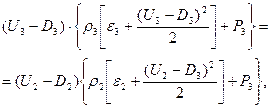
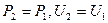
Используя формулу (14), из первых трех уравнений системы (15) получаем, что
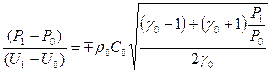 ,
,
а из четвертого, пятого и шестого уравнений –
 . (16)
. (16)
Где 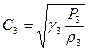 - скорость звука в области «3».
- скорость звука в области «3».
Заменяя в (16) 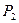 на
на 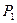 и
и 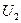 на
на 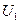 , приходим к системе из двух уравнений с двумя неизвестными
, приходим к системе из двух уравнений с двумя неизвестными 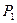 и
и 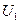 :
:
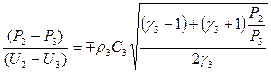
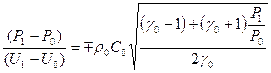
Введем обозначения 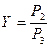 ;
; 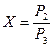 ;;
;; 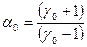
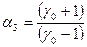 .
.
Умножим первое уравнение (17) на 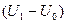 и поделим на первую часть, а затем аналогично второе уравнение (17) умножим на
и поделим на первую часть, а затем аналогично второе уравнение (17) умножим на 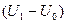 и разделим на первую часть.
и разделим на первую часть.
Возведем в квадрат первое и второе уравнения (18) и вычтем из второго первое.
 (19)
(19)
Подставляя в (19) вчесто  и
и  их выражения из (18) и сокращая на общий множитель, получим
их выражения из (18) и сокращая на общий множитель, получим
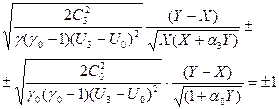 (20)
(20)
Затем еще раз возведем в квадрат, но уже равенство (20):
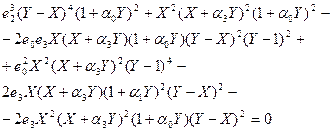 (23)
(23)
Если в (23) привести подобные члены и сгруппировать их при одинаковых степенях  , то получим алгебраическое уравнение шестой степени:
, то получим алгебраическое уравнение шестой степени:
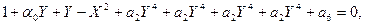 (24)
(24)
Перенесем из правой части (30) первое слагаемое влево, возведем в квадрат и умножим на знаменатель:
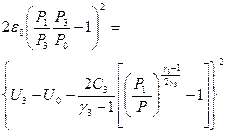 (31)
(31)
Где 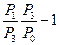 - начальная удельная внутренняя энергия в правом полупространстве.
- начальная удельная внутренняя энергия в правом полупространстве.
Если ввести обозначения 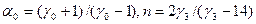 ;
;
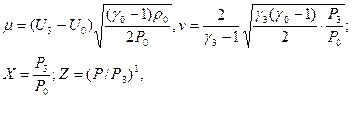
Тогда уравнение (31) можно записать в виде
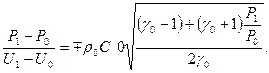
Или раскрывая скобки и приводя подобные члены,
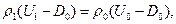
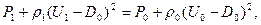
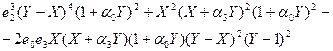
В результате исследования двух вариантов распада газодинамического разрыва удалось системы нелинейных уравнений второго и восьмого порядка свести к одному алгебраическому уравнению с действительными коэффициентами. К вопросам нахождения корней алгебраических уравнений вернемся после изучения случаев распада разрывов с уравнением состояния, отличным от уравнения состояния идеального газа.
| <== предыдущая страница | | | следующая страница ==> |
| ТЕХНОХИМИЧЕСКИЙ КОНТРОЛЬ ПРОИЗВОДСТВА | | |
Дата добавления: 2014-11-24; просмотров: 332; Нарушение авторских прав

Мы поможем в написании ваших работ!