
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
ВЫЧИСЛЕНИЯ С ИСПОЛЬЗОВАНИЕМ СТЕКА
11.1 Ключевые (основные) вопросы (моменты)
— понятие о стековом процессоре;
— особенности формата команд стекового процессора.
11.2 Текст лекции
11.2.1 Вычисления с использованием стека
Число адресов в команде определяется принятой в вычислительной машине системой адресации: трехадресный формат команды позволяет задать адреса двух операндов и адрес ячейки, куда заносится результат операции, двухадресный формат команды предполагает, что адресом результата является адрес одного из операндов. Переход к одноадресному формату требует выделения определенного стандартного места для хранения первого операнда и результата, для чего обычно используется специальный регистр, называемый аккумулятором. Безадресный формат используется в случае команд, не требующих операндов, или если для операндов определено местоположение, такое как стек.
Для работы со стеком используются значения трех адресов памяти: адрес основания стека, то есть начальный адрес области памяти, выделенной под стек; граничный адрес стека, содержащий адрес другой границы области памяти; адрес вершины стека, указывающий на текущий верхний элемент. В большинстве вычислительных машин основание стека располагается в области старших адресов выделенной области памяти и указатель стека при добавлении в стек элементов смещается в сторону младших адресов.
Представляя собой упорядоченное множество элементов данных, только один из которых, размещенный в вершине стека, может быть доступен при обращении, стек использует дисциплину обслуживания в обратном порядке (LIFO, Last In First Out), при которой элементы добавляются в вершину стека и удаляются из нее. При выполнении бинарных операций два верхних элемента выбираются из стека в качестве операндов, а результат операции помещается обратно в вершину стека. Унарные операции, требующие только одного операнда, используют только один верхний элемент. В целях повышения быстродействия верхние ячейки стековой памяти, где хранятся операнды и куда заносится результат операции, делаются более быстродействующими и размещаются в процессоре, в то время как остальная часть стека располагается в основной памяти.
Таким образом, стек не только используется при выполнении управляющих команд в рассмотренном ранее процессе обслуживания вызовов подпрограмм или в системах прерывания, но и при вычислении арифметических и логических выражений. Вычислительные машины с архитектурой системы команд на базе стека называют стековыми. Специфика стековых машин заключается, прежде всего, в необходимости специальных подходов к программированию, связанных с представлением арифметических выражений в постфиксной форме и введением специальной команды, дублирующей содержимое верхнего элемента стека вниз для решения проблемы хранения промежуточных результатов. Для работы со стеком в систему команд процессора включаются специальные команды, которые осуществляют запись в стек (push) содержимого ячейки памяти и сохраняют содержимое стека (pop) в основной памяти.
При описании вычислений с использованием стека применяется форма записи математических выражений, известная как обратная польская запись, которая была предложена в 50-х годах польским математиком Яном Лукасевичем (J. Lukasiewicz). Особенность польской нотации в том, что для представления арифметических выражений используется не привычная инфиксная (infix) форма, в которой знак операции располагается между операндами и для указания порядка вычислений используются скобки, а постфиксная (postfix) форма, при которой в выражении скобки отсутствуют, а знак операции следует за операндами.
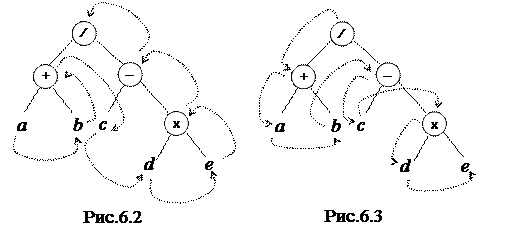 Рассмотрим сущность обратной польской записи на примере. Арифметическое выражение (a + b)/ (c – d x e) представим в виде дерева, в котором левая ветвь каждого узла отвечает левому операнду, а правая – правому (рис.6.2). В каждой ветви операциям, которые выполняются раньше, соответствуют нижележащие узлы. Верхний узел, с которого начинается построение дерева (корень дерева), отвечает операции, которая выполняется последней.
Рассмотрим сущность обратной польской записи на примере. Арифметическое выражение (a + b)/ (c – d x e) представим в виде дерева, в котором левая ветвь каждого узла отвечает левому операнду, а правая – правому (рис.6.2). В каждой ветви операциям, которые выполняются раньше, соответствуют нижележащие узлы. Верхний узел, с которого начинается построение дерева (корень дерева), отвечает операции, которая выполняется последней.
Если, начав с нижнего листа самой левой ветви дерева, обойти все листья и узлы дерева так, чтобы ветви рассматривались слева направо, а узел рассматривался только после обхода всех исходящих из него ветвей, как показано стрелками на рис.6.2, то получим обратную польскую запись исходного выражения: a b + c d e x – /.
Польская запись не требует учитывать приоритет операций, в ней знаки операций следуют строго в порядке их выполнения, а операнды располагаются в том же порядке, что в исходном выражении. Отсюда следует основное преимущество обратной польской записи перед обычной записью выражений со скобками: выражение можно вычислить в процессе однократного просмотра слева направо. Это упрощает создание компилятора, однако, поскольку не предполагается произвольного доступа к памяти, в данном методе вычислений затруднительна оптимизация выражений.
Правило вычисления выражения в обратной польской записи состоит в следующем: обратная польская запись просматривается слева направо и если встречается операнд, то он помещается в стек; если рассматриваемый элемент – знак унарной операции, то операнд выбирается из стека, над ним выполняется операция, а результат записывается в стек; если встречается знак бинарной операции, то два операнда выбираются из стека и после выполнения операции результат помещается в стек. Правым операндом выполняемой операции является число, находящееся на вершине стека.
В результате последовательного выполнения этого алгоритма будут выполнены все операции, имеющиеся в выражении, и в стеке окажется конечный результат вычислений r, равный (a+b)/(c–dxe). Последовательность действий для рассматриваемого примера, а также программа для машины с безадресной системой команд, представлены на рис.6.4.
| ШАГ | Оставшаяся цепочка | Команда | Стек Вершина↓ стека | |||
| 1 | a b + c d e x – / | push a | a | |||
| 2 | b + c d e x – / | push b | a | b | ||
| 3 | + c d e x – / | add | a+b | |||
| 4 | c d e x – / | push c | a+b | c | ||
| 5 | d e x – / | push d | a+b | c | d | |
| 6 | e x – / | push e | a+b | c | d | e |
| 7 | x – / | mul | a+b | c | d x e | |
| 8 | – / | sub | a+b | c – dxe | ||
| 9 | / | div | r | |||
| 10 | pop r |
Рис.6.4
Преобразование в постфиксную форму с последующим формированием последовательности машинных команд, реализующих вычисления по данному алгоритму, применяется в большинстве компиляторов с языков высокого уровня, в которых применяется инфиксная форма записи выражений. Несмотря на то, что программы для вычислительных машин с одноадресной и двухадресной системой команд не соответствуют строго сформулированным выше правилам, при их формировании используется похожий алгоритм.
Известно несколько методов перевода инфиксных формул в обратную польскую запись. Один из наиболее эффективных методов был предложен в 1960 году голландским ученым Э. Дейкстрой (Edsger W. Dijkstra). Метод Дейкстры основан на использовании стека с приоритетами, позволяющего изменить порядок следования знаков операций в выражении так, что получается обратная польская запись. В данном методе каждому ограничителю, входящему в выражение, присваивается приоритет. Для знаков операций приоритеты возрастают в порядке, обратном старшинству операций, левая скобка имеет низший (нулевой) приоритет.
Арифметическое или логическое выражение рассматривается как входная строка символов слева направо. Операнды переписываются в выходную строку, а знаки операций вначале помещаются в стек операций. Если приоритет входного знака равен нулю или больше приоритета знака, находящегося в вершине стека, то новый знак добавляется к вершине стека. В противном случае из стека выталкивается и переписывается в выходную строку знак, находящийся в вершине, а также следующие за ним знаки с приоритетами, большими или равными приоритету входного знака. После этого входной знак добавляется к вершине стека.
Особенности имеет обработка скобок: открывающаяся скобка просто записывается в вершину стека, не выталкивая ни одного знака, в тоже время её не может вытолкнуть ни один знак, кроме закрывающейся скобки. Появление закрывающей скобки, имеющей первый приоритет, не превышающей приоритет любой операции, вызывает выталкивание всех знаков до ближайшей открывающей скобки включительно. В стек закрывающая скобка не заносится, взаимно уничтожаясь с открывающей скобкой. После просмотра всех символов входной строки происходит выталкивание всех оставшихся в стеке символов и дописывание их к выходной строке.
Процесс получения обратной польской записи для выражения (a+b)/(c–dxe) представлен на рисунке 6.5.
| Символ | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| Входная строка | ( | a | + | b | ) | / | ( | c | – | d | x | e | ) | ||
| Вершина стека → Стек операций | ( | + | + | / | ( | ( | – | – | x | x | – | / | |||
| ( | ( | / | / | ( | ( | – | – | ( | |||||||
| / | / | ( | ( | / | |||||||||||
| / | / | ||||||||||||||
| Выходная строка | a | b | + | c | d | e | x | – | / |
Рис.6.5
Существует еще одна форма бесскобочной записи выражений, называемая префиксной (prefix) формой или прямой польской записью. При префиксной записи операнды также расположены в том же порядке, что в исходном выражении, однако знаки операций записываются перед своими операндами. Выражение, записанное в прямой польской записи, вычисляется справа налево и может быть получено при обходе дерева, начиная с верхнего узла так, чтобы сразу после рассмотрения очередного узла просматривались слева направо исходящие из него ветви, как показано стрелками на рис.6.3. В этом случае дерево представляется в виде: / + a b – c x d e.
Префиксная форма используется для записи функций в языках программирования: для обращения к функции в программе имя функции пишется перед ее аргументами. Используя префиксную запись можно вычислить любое выражение за один просмотр, однако при этом необходимо знать количество аргументов для каждой операции. Поэтому, например, в языке функционального программирования LISP для поддержки языковых средств обработки списков используется один из вариантов этого способа записи, который иногда называют кембриджской польской записью. В этой записи операция и ее аргументы заключаются в скобки, и выражение принимает вид вложенного множества списков, в котором каждый список начинается с символа операции, за которым следуют списки, представляющие ее операнды. В кембриджской польской записи рассматриваемое выражение выглядит следующим образом:
(/ (+ a b)(– c (x d e))).
С использованием стека связана идея стековой выборки команд, предполагающая реализацию в виде стека буфера команд устройства управления. В этом случае в устройстве управления явно отсутствует регистр адреса команды, так как очередная команда выбирается из верхнего элемента стека. Возникающая при этом проблема выполнения команды перехода по адресу решается посредством использования циклического стека с адресацией.
12 Лекция №11
| <== предыдущая страница | | | следующая страница ==> |
| Ассоциативный процессор | | |
Дата добавления: 2014-11-24; просмотров: 689; Нарушение авторских прав

Мы поможем в написании ваших работ!