Уравнения относительного движения

Получим уравнения движения материальной точки в неинерциальной системе отсчета. Для этого воспользуемся теорией сложного движения точки, рассматривая ее движение одновременно в двух системах координат – основной 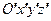(инерциальная система отсчета) и подвижной .

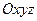Пусть 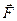- равнодействующая сил, действующих на точку M.

В инерциальной системе отсчета: _.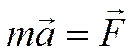

Воспользуемся выражением для абсолютного ускорения точки (теорема Кориолиса): 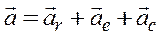. Тогда

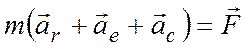, или .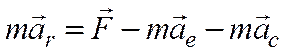

Величины 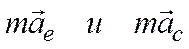имеют размерность силы. Вводя обозначения: 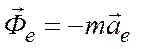- переносная сила инерции, 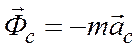- кориолисова сила инерции,получаем

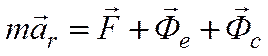- основное уравнение динамики

относительного движения.

Уравнение движения в подвижной системе координат не совпадает с основным уравнением динамики, следовательно, соответствующая система отсчета не является инерциальной.

Итак, чтобы получить уравнение движения точки в неинерциальной системе отсчета, необходимо добавить переносную и кориолисову силы инерции.

Дифференциальные уравнения относительного движения материальной точки имеют вид:

,

,

.

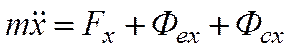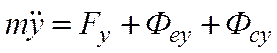Если подвижная система координат движется поступательно, равномерно и прямолинейно, то переносная и кориолисова силы инерции равны нулю и относительное движение описывается основным уравнением динамики. Это выражает принцип относительности классической механики, заключающийся в том, что уравнения движения не зависят от того, относить ли их к неподвижным осям или подвижным, перемещающимся поступательно, равномерно и прямолинейно.

[1] Галилей Галилео (15.02.1564-8.01.1642) − итальянский физик, механик, математик, астроном, один из основателей точного естествознания. Исследования по статике, динамике и механике материалов.

[2] Ньютон Исаак (4.01.1643-31.03.1727) − английский математик, физик, механик, астроном, основоположник современной механики, член и президент Лондонского королевского общества, иностранный член Парижской АН. Открыл закон всемирного тяготения, создал теоретические основы механики и астрономии, разработал дифференциальное и интегральное исчисление. Также работы по теоретической и экспериментальной оптике, по геометрии и алгебре.

[3] Кеплер Иоганн (27.12.1571-15.11.1630) − немецкий астроном, математик и механик. Вывел два первых закона движения планет. Положил начало небесной механике.

Дата добавления: 2014-02-27; просмотров: 437; Нарушение авторских прав

Мы поможем в написании ваших работ!