
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Материальной точки
Дифференциальные уравнения движения
Основные задачи динамики
Инерциальные системы отсчета
Система отсчета, в которой выполняются первый и второй законы динамики, называется инерциальной системой отсчета.
Инерциальность той или иной системы отсчета может быть проверена только опытным путем.
Для большинства технических задач за такую систему можно взять систему координат, связанную с Землей.
Первая задача динамики
Определение сил, действующих на материальную точку, если известна масса точки и закон ее движения.
Вторая задача динамики
Определение закона движения материальной точки при известной массе и силах, действующих на точку.
Примером решения первой и второй задач динамики служит аналитический вывод Ньютона силы всемирного тяготения из законов движения планет Кеплера[3] и решение обратной задачи – получение законов Кеплера при известной силе всемирного тяготения.
Воспользуемся основным уравнением динамики 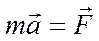 , из закона независимости действия сил:
, из закона независимости действия сил: 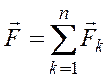 - равнодействующая всех сил.
- равнодействующая всех сил.
В общем случае силы, действующие на точку, являются переменными. Тогда в проекциях на оси декартовой системы координат можно записать:
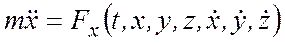 ,
,
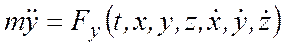 ,
,
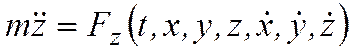 .
.
Эти уравнения содержат производные координат и образуют систему дифференциальных уравнений движения материальной точки.
Общее решение этих уравнений содержит шесть произвольных постоянных:
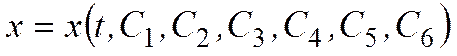 ,
,
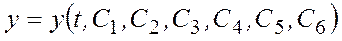 ,
,
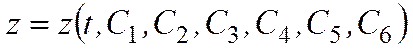 .
.
Произвольные постоянные находятся из начальных условий:
 ,
, 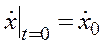 ,
,
 ,
, 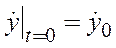 ,
,
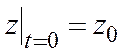 ,
, 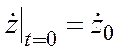 .
.
Если точка движется по известной траектории, то основное уравнение динамики удобно записать в проекциях на оси естественной системы координат. В этом случае:
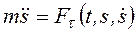 ,
,
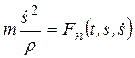 ,
,
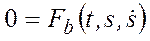 .
.
Правые части этих уравнений содержат неизвестные силы реакций связей, так как движущаяся точка несвободна. Исследование движения предполагает одновременное решение первой и второй задач динамики при следующих начальных условиях:
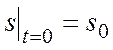 ,
, 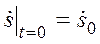 .
.
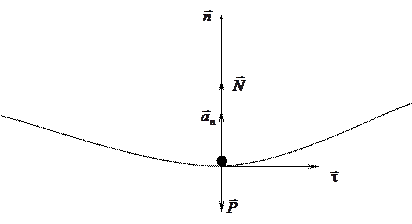 |
| <== предыдущая страница | | | следующая страница ==> |
| Законы Галилея-Ньютона | | | Уравнения относительного движения |
Дата добавления: 2014-02-27; просмотров: 458; Нарушение авторских прав

Мы поможем в написании ваших работ!