КИНЕМАТИКА ТОЧКИ

Единицей измерения длины в СИ является метр (м). Первоначально за метр была принята длина, равная одной десятимиллионной части четверти земного меридиана. В настоящее время: 1 метр – длина пути прохождения светом в вакууме в течение временного интервала 1/299792458 с.

Системой отсчета называют тело отсчета, жестко связанную с ним систему координат и часы.

Единицей измерения времени в СИ (система интернациональная) является секунда(с). Первоначально секунда была принята за интервал времени, равный 1/86400 средних солнечных суток. В настоящее время: 1 секунда – промежуток времени, в течении которого совершается 9 192 631 770 периодам электромагнитного излучения, соответствующего переходу между двумя сверхтонкими уровнями основного состояния атома цезия-133 в отсутствии внешних полей.

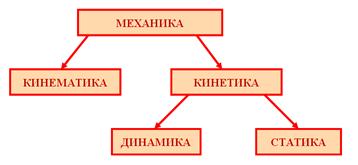Механика состоит из следующих разделов: кинематика и кинетика. Кинематика изучает механическое движение без исследования причин, которые это движение вызывают.

Кинетика состоит из динамики и статики. В динамике изучаются причины, которые вызывают механическое движение. Законы равновесия тел изучаются в статике.

Способы задания движения точки

Под точкой в кинематике понимают геометрическую точку. Движение точки можно задать тремя способами.

КООРДИНАТНЫЙ СПОСОБ

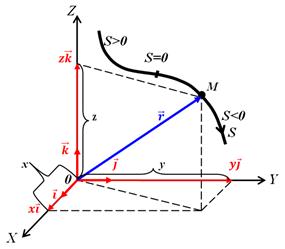Рассмотрим движение точки М. Для определения положения точки М в декартовой системе координат достаточно задать ее координаты. Под координатами данной точки будем понимать координаты той точки пространства, с которой совпадает эта точка.

Если положение точки М с течением времени относительно системы координат XYZ меняется, то координаты являются функциями времени:

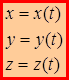(1.1)

Уравнения (1.1) называются кинематическими уравнениями движения точки.

Функции x(t), y(t), z(t) должны быть:

- однозначными (т.к. конкретному моменту времени соответствует единственное положение точки в пространстве);

- дважды дифференцируемыми (точка в любой момент времени должна иметь определенные скорость и ускорение).

Траекторией точки называют геометрическое место точек пространства, через которое точка проходит в процессе движения. Чтобы получить уравнение траектории нужно из системы уравнений (1.1) исключить время.

ВЕКТОРНЫЙ СПОСОБ

При этом способе положение точки определяется радиусом-вектором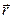, начало которого совпадает с началом системы координат XYZ, а конец – с той точкой пространства, в которой располагается точка. Если точка движется с течением времени относительно системы координат, то 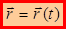– кинематическое уравнение движении точки.

Разложив радиус-вектор по ортам, получим:

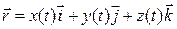, (1.2)

где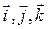– единичные вектора: .

ЕСТЕСТВЕННЫЙ СПОСОБ

Пусть известна траектория точки. В этом случае можно поступить так: на траектории выбирают начало отсчета 0 и задают направление увеличения естественной координатыS.

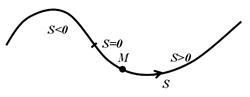При движении точки вдоль траектории ее естественная координата зависит от времени:

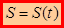–кинематическое уравнение движения(закон движения точки по траектории).В этом случае зависимость радиуса-вектора от времени можно записать в виде сложной функции: .

Дата добавления: 2014-03-11; просмотров: 439; Нарушение авторских прав

Мы поможем в написании ваших работ!