
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Скорость точки и ее нахождение при различных способах движения точки
Важным параметром, характеризующим движение, является скорость перемещения точки. Для определения этого понятия рассмотрим движение точки, заданное векторным уравнением:
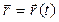 . (1.3)
. (1.3)
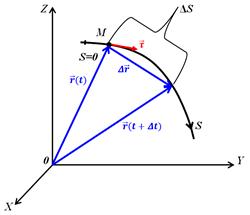
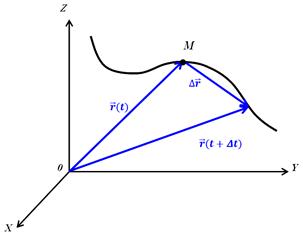 Пусть в некоторый момент времени t положение точки М определяется радиусом-вектором
Пусть в некоторый момент времени t положение точки М определяется радиусом-вектором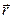 . За промежуток времени ∆t точка перемещается в положение, определяемое радиусом-вектором
. За промежуток времени ∆t точка перемещается в положение, определяемое радиусом-вектором 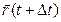 . Вектор, характеризующий перемещение точки характеризующий перемещение точки
. Вектор, характеризующий перемещение точки характеризующий перемещение точки 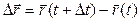 .
.
Составим отношение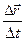 . Вычислим предел этого отношения в предположении, что промежуток времени
. Вычислим предел этого отношения в предположении, что промежуток времени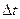 стремиться к нулю:
стремиться к нулю:
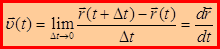 – скорость точки в момент времени t. Скорость
– скорость точки в момент времени t. Скорость 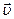 равна первой производной по времени от радиус-вектора.
равна первой производной по времени от радиус-вектора.
Научимся вычислять скорость при трёх способах задания движения.
ПРИ ВЕКТОРНОМ СПОСОБЕ
Задано 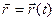 . Исходя из определения скорости, при векторном способе она определяется соотношением:
. Исходя из определения скорости, при векторном способе она определяется соотношением:
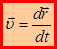 (1.4)
(1.4)
ПРИ КООРДИНАТНОМ СПОСОБЕ
Ранее было записано разложение радиус-вектора 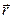 по ортам:
по ортам:
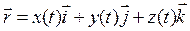 (1.5)
(1.5)
Также по ортам можно разложить скорость точки:
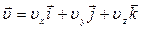 . (1.6)
. (1.6)
Используя (1.4), получим:
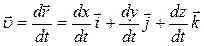 ,
,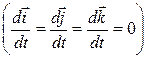 . (1.7)
. (1.7)
Сравнивая (1.6) и (1.7), и зная, что для равенства двух векторов необходимо и достаточно равенство их соответствующих проекций:
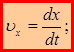
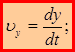
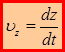 . (1.8)
. (1.8)
Модуль вектора скорости определяется по формуле:
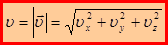 (1.9)
(1.9)
Направление скорости определяется направляющими косинусами вектора 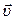 :
:
 (1.10)
(1.10)
ПРИ ЕСТЕСТВЕННОМ СПОСОБЕ
 Задано S=S(t).Находим:
Задано S=S(t).Находим: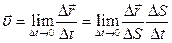
При 
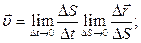
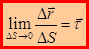 – единичный вектор касания.
– единичный вектор касания.
По определению 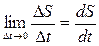 . Следовательно:
. Следовательно:
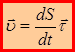 (1.11)
(1.11)
Величина 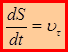 есть проекция скорости на естественную координату
есть проекция скорости на естественную координату 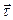 .
.
Модуль скорости , т.к.
, т.к.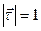 ; тогда
; тогда
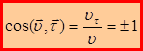 , (1.12)
, (1.12)
т.е. скорость направлена по касательной к траектории (в ту же или противоположную сторону направления вектора касания 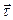 ).
).
| <== предыдущая страница | | | следующая страница ==> |
| КИНЕМАТИКА ТОЧКИ | | | Ускорение точки и его нахождение при различных |
Дата добавления: 2014-03-11; просмотров: 410; Нарушение авторских прав

Мы поможем в написании ваших работ!