
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Ускорение точки и его нахождение при различных
способах задания движения
При движении точки её скорость, вообще говоря, изменяется со временем. Поэтому необходимо ввести величину, которая полностью смогла бы охарактеризовать изменение скорости. Для этого рассмотрим движение точки М, заданное в виде: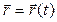 .
.
 Наглядность поведения
Наглядность поведения 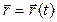 достигается тем, что радиус-векторы точки М имеют начало в одной точке 0. Изменения вектора
достигается тем, что радиус-векторы точки М имеют начало в одной точке 0. Изменения вектора 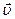 так наглядно не изображается, т.к. эти векторы приложены к различным точкам траектории.
так наглядно не изображается, т.к. эти векторы приложены к различным точкам траектории.
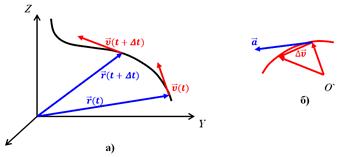
Выберем какую-либо точку О’ и перенесём все векторы скорости параллельно самим себе, так чтобы их начала совпадали с точкой О’. Тогда концы вектора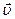 с течением времени определят непрерывную (т.к. вектор
с течением времени определят непрерывную (т.к. вектор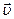 изменяется непрерывно) кривую, называемую годографом вектора скорости. На рис б) непрерывной линией изображён годограф вектора скорости. Аналогично этому траекторию точки называют годографом радиуса-вектора. Вектор
изменяется непрерывно) кривую, называемую годографом вектора скорости. На рис б) непрерывной линией изображён годограф вектора скорости. Аналогично этому траекторию точки называют годографом радиуса-вектора. Вектор
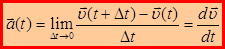 – ускорение точки в момент времени t.(1.13)
– ускорение точки в момент времени t.(1.13)
Научимся вычислять скорость при трёх способах задания движения.
ПРИ ВЕКТОРНОМ СПОСОБЕ
Задано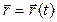
Исходя из определения ускорения, при векторном способе оно определяется соотношением: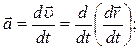 .
.
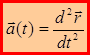 (1.14)
(1.14)
ПРИ КООРДИНАТНОМ СПОСОБЕ
Задано:
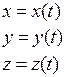
Разложим 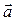 по ортам:
по ортам:
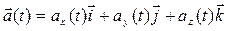 (1.15)
(1.15)
С другой стороны, из (1.14) следует:
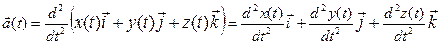 , (1.16)
, (1.16)
поскольку 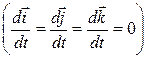 .
.
Для равенства двух векторов необходимо и достаточно, чтобы были равны их проекции. Сравнивая (1.15) и (1.16):
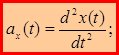
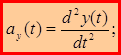
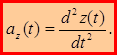 (1.17)
(1.17)
Модуль ускорения находится по формуле:
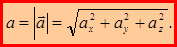 или
или 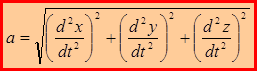 (1.18)
(1.18)
Направляющие косинусы:
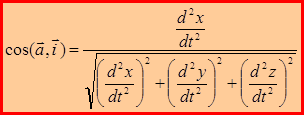 ;
;
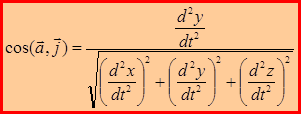 ; (1.19)
; (1.19)
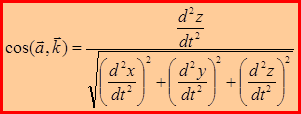 .
.
ПРИ ЕСТЕСТВЕННОМ СПОСОБЕ
Задано S=S(t). Скорость при естественном способе задания движения 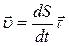 . По определению ускорения:
. По определению ускорения:
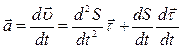 . (1.20)
. (1.20)
Направление вектора 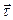 зависит от значения естественной координаты S. Поскольку
зависит от значения естественной координаты S. Поскольку 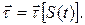 , то:
, то: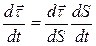 (1.21)
(1.21)
Подставляя (1.21) в (1.20): 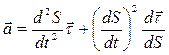 (1.22)
(1.22)
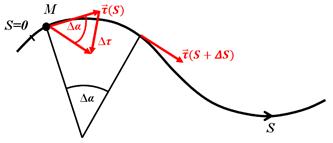
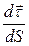 – определяется лишь характером кривой линии:
– определяется лишь характером кривой линии: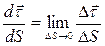 . Угол между касательными называют углом смежности (
. Угол между касательными называют углом смежности (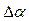 – угол смежности).
– угол смежности).
Выясним направление вектора 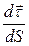 .Устремим ∆S→ 0. Вектор
.Устремим ∆S→ 0. Вектор 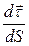 ┴
┴ направлен в сторону вогнутости кривой. Нормаль, лежащая в соприкасающейся плоскости называется главной нормалью. Найдем модуль
направлен в сторону вогнутости кривой. Нормаль, лежащая в соприкасающейся плоскости называется главной нормалью. Найдем модуль 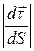 :
: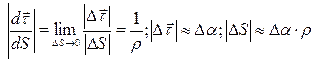 . Отсюда
. Отсюда 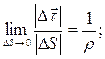 где
где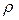 – радиус кривизны траектории в рассматриваемой точке М.
– радиус кривизны траектории в рассматриваемой точке М.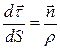 , где
, где 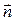 - единичный вектор главной нормали, направлен в сторону вогнутости траектории.
- единичный вектор главной нормали, направлен в сторону вогнутости траектории.
После подстановки в (1.22):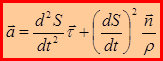 (1.23)
(1.23)
Составляющие ускорения определяют как: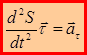 – тангенциальное ускорение.
– тангенциальное ускорение.
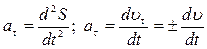 – данный результат получен с учетом (1.12).
– данный результат получен с учетом (1.12).
Если 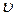 =const, то
=const, то 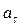 = 0, следовательно
= 0, следовательно 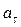 – отвечает за изменение модуля скорости;
– отвечает за изменение модуля скорости; 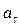 = 0 – только при равномерном движении (движение при
= 0 – только при равномерном движении (движение при 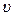 =const);
=const); 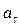 – к форме траектории никакого отношения не имеет.
– к форме траектории никакого отношения не имеет.
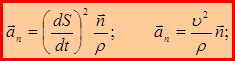
 – нормальное ускорение.
– нормальное ускорение.
Нормальное ускорение 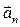 определяет форму траектории и направлено в сторону вогнутости кривой. При прямолинейном движении
определяет форму траектории и направлено в сторону вогнутости кривой. При прямолинейном движении 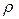 → ∞ и
→ ∞ и 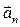 =0.
=0.
| <== предыдущая страница | | | следующая страница ==> |
| Скорость точки и ее нахождение при различных способах движения точки | | | Частные случаи движения точки |
Дата добавления: 2014-03-11; просмотров: 491; Нарушение авторских прав

Мы поможем в написании ваших работ!