Интервальные оценки

Интервальное оценивание особенно необходимо при малом количестве наблюдений, когда точечная оценка малонадежна.

Интервальной называют оценку, которая определяется двумя числами – концами отрезков.

Оценивание с помощью доверительного интервала – это способ оценки, при котором с заданной доверительной вероятностью g устанавливают границы доверительного интервала.

Задачу интервального оценивания в самом общем виде можно сформулировать так: по данным выборки построить числовой интервал, относительно которого с заранее выбранной вероятностью можно сказать, что этот интервал покроет (накроет) оцениваемый параметр. Выбор значения доверительной вероятности не является математической задачей, а определяется конкретной решаемой проблемой.

Доверительным интервалом для параметра Q называется такой интервал, относительно которого можно с заранее выбранной вероятностью

g = 1 – a (9.6)

(близкой к единице), утверждать, что он содержит неизвестное значение параметра Q; a – уровень значимости.

Пусть Q^* – несмещенная оценка параметра Q. Требуется оценить возможную при этом ошибку. По определенным правилам находят такое число d > 0, чтобы выполнялось соотношение:

P (|Q^*– Q| < d) = g или P (Q_min < Q < Q_max) = g. (9.7)

Равенство означает, что интервал [Q_min; Q_max], где Q_min = Q^* – d, а Q_max = Q^* + d, заключает в себе оцениваемый параметр с доверительной вероятностью g .

Нижняя и верхняя граница доверительного интервала Q₁ и Q₂ определяются по результатам наблюдений, следовательно, сам доверительный интервал является случайной величиной. В связи с этим говорят, что доверительный интервал покрывает оцениваемый параметр с вероятностью g.

Надежность принято выбирать равной 0,95; 0,99; 0,999 – тогда событие, состоящее в том, что интервал [Q_min; Q_max], покрывает параметр Q будет практически достоверным.

При этом число d характеризует точность интервальной оценки: чем меньше d, тем оценка точнее и наоборот.

9.1.2.1. Интервальная оценка математического ожидания при известной дисперсии.

Пусть случайная величина Х Î N (М[Х]; D[Х] ) распределена по нормальному закону, причем математическое ожидание неизвестно, а дисперсия D[Х] = s² известна. Требуется оценить неизвестное математическое ожидание. По наблюдениям найдем точечную оценку М[Х]^* математического ожидания. Зададимся вероятностью g и найдем такое число d, чтобы выполнялось соотношение:

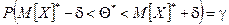. (9.8)

Доказано, что построение доверительного интервала в этом случае осуществляется по формуле:

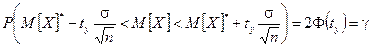, (9.9)

где t_у – значение стандартной нормальной величины, соответствующее надежности 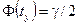, а Ф(t_у) – функция Лапласа; s – среднее квадратическое отклонение.

Очевидно, что увеличение надежности g приводит к увеличению функции Ф(t_у) и соответственно увеличению параметра t_у, что в свою очередь увеличивает величину d. То есть увеличение надежности оценки ведет к снижению ее точности (увеличению погрешности).

При этом точность оценки математического ожидания равна:

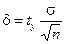. (9.10)

Очевидно, что с увеличением объема выборки n величина погрешности d уменьшается, т.е. точность оценки повышается.

Формула (9.10) позволяет определить необходимый объем выборки для оценки математического ожидания с наперед заданной точностью и надежностью:

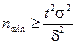. (9.11)

Смысл формулы (9.8) состоит в следующем: с надежностью g доверительный интервал 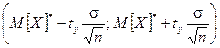покрывает неизвестный параметр М[Х]^*генеральной совокупности. Можно сказать иначе: точечная оценка М[Х]^* определяет значение параметра Х генеральной совокупности с точностью 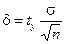и надежностью g.

В результате можно сформулировать алгоритм отыскания границ доверительного интервала для математического ожидания, если известна дисперсия D [Х] = s²:

1. Задать значение надёжности – g.

2. По величине 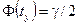выбрать значение t_у из таблицы для функции Лапласа.

3. Вычислить точность оценки математического ожидания

4. Записать доверительный интервал по формуле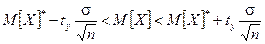

Каждому доверительному интервалу соответствует свое критическое значение. Например, для g = 0,95 t _у = ± 1,96, а для g = 0,99 и a = 0,01 t _у = ± 2,58.

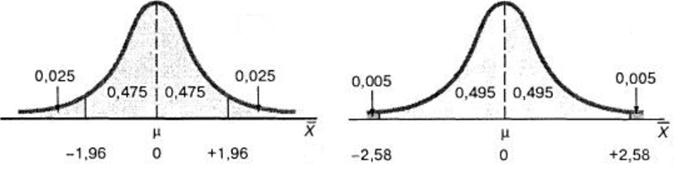
Рис. 9.1. Гауссова кривая для g = 0,95 и g = 0,99

Пример 9.1. Случайная величина имеет нормальное распределение. Найти доверительные интервалы для оценки с надежностью 0,96 неизвестного математического ожидания а, если объем выборки n = 49, генеральное среднее квадратическое отклонение s = 5; выборочная средняя М[X]^* = 30.

Решение.

Поскольку g = 0,96, то Ф(t_g) = g/2 = 0,48. По табл. функции Лапласа находим для Ф(t_g) = 0,48 t_g = 2,06.

Точность оценки математического ожидания:

,

.

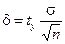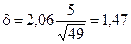28,53 < М [X]^*< 31,47.

Пример 9.2. Имеется генеральная совокупность с некоторой характеристикой, распределенной по нормальному закону. Дисперсия равна 6,25. Выборка имеет объем n = 27. Получено средневыборочное значение характеристики `х = 27. Найти доверительный интервал с надежностью g = 0,99, покрывающий неизвестное математическое ожидание исследуемой характеристики.

Решение. Для Ф(t_g) = 0,99/2 = 0,495 t_g = 2,58.

,

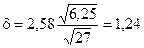Отсюда, доверительный интервал (10,76; 13,24).

Пример 9.3. Найти минимальный объем выборки n, при котором с надежностью 0,95 можно утверждать, что точность оценки математического ожидания M[X], по выборочному среднему арифметическому равна d = 0,2, если известно, что среднее квадратическое отклонение s = 2,0. Предполагается, что выборка величины нормально распределена.

Решение: По таблице находим, что при Ф(t) = 0,95/2 = 0,475 t = 1,96.

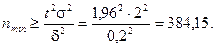
Значит, объем выборки должен бать не менее 385.

Дата добавления: 2014-11-24; просмотров: 515; Нарушение авторских прав

Мы поможем в написании ваших работ!