Оценка математического ожидания

Пусть имеется случайная величина Х с математическим ожиданием М[Х] и дисперсией D[Х], при этом оба параметра неизвестны. Над величиной Х произведено N независимых экспериментов, в результате которых была получена совокупность численных результатов х₁, х₂,…, х_N.

В качестве оценки математического ожидания естественно предположить среднее арифметическое наблюдаемых значений:

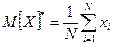. (9.2)

Оценка математического ожидания является несмещенной.

Например, одним прибором (без систематических ошибок) сняли показания случайной величины, т.е. х₁ = 13, х₂ = 15, х₃ = 17. Простая несмещенная оценка математического ожидания cоставит М[Х]^* = (13 + 15 + 17)/3 = 15. (т.е. это среднее значение наблюдаемой величины).

Оценка дисперсии.

Дисперсия характеризует меру разброса около ее среднего значения (мера рассеивания, т.е. отклонения от среднего).

При больших объемах выборки для оценки дисперсии используют формулу выборочной дисперсии

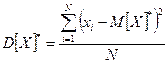. (9.3)

Для случая предыдущего примера:

D[Х]* = ((13 – 15)² + (15 – 15) ² + (17 – 15) ²)/3 = 8/3 = 2,67.

Это смещенная оценка генеральной дисперсии.

Для получения несмещенной оценки дисперсии генеральной совокупности, нужно умножить выборочную дисперсию на 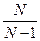. Тогда получиться величина, называемая исправленной выборочной дисперсией

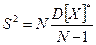. (9.4)

Выражение для исправленной дисперсии является несмещенной оценкой генеральной дисперсии

А оценку среднего квадратического отклонения (стандарта) осуществляют по формуле:

S* = ÖS² . (9.5)

S² = 3 × 2,67/(3 – 1) = 4.

Точечные оценки параметров генеральной совокупности могут быть приняты в качестве ориентировочных, первоначальных результатов обработки выборочных данных.

Дата добавления: 2014-11-24; просмотров: 236; Нарушение авторских прав

Мы поможем в написании ваших работ!