Интервальная оценка математического ожидания при неизвестной дисперсии

На практике как математическое ожидание генеральной совокупности, так и его отклонение часто бывают неизвестными.

Ирландским статистиком Уильямом С. Госсетом было предложено t-распределение Стьюдента, позволившее разрешить проблему оценивания математического ожидания при неизвестной дисперсии.

Внешне график этого распределения очень напоминает стандартизованное нормальное распределение (представляет собой колокообразную форму и является симметричным).

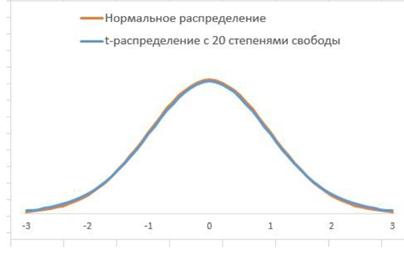
Рис. 9.2. Стандартизованное нормальное распределение и t-распределение Стьюдента с различным числом степеней свободы

В результате по наблюдениям находятся точечные оценки математического ожидания и дисперсии.

В этом случае построение доверительного интервала осуществляется по формуле:

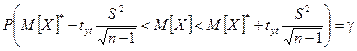(9.12)

где t_gt – значение функции распределения Стьюдента (t-распределения), соответствующее степеням свободы k = n – 1 и надежности g.

При этом точность оценки математического ожидания равна: .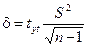

Из уравнений видно, что распределение Стьюдента определяется числом степеней свободы и не зависит от неизвестных параметров математического ожидания и среднеквадратического отклонения.

Пример 9.4. Случайная величина Х имеет нормальное распределение. По выборке объема n = 61 найдена выборочная средняя M[X]^* = 30 и исправленное среднее квадратичное значение S² = 1,5. Найти доверительный интервал для оценки с надежностью g = 0,95 неизвестного математического ожидания.

Решение:

Определим число степеней свободы k = n – 1 = 61 – 1 = 60.

Уровень значимости a = 1 – g = 1 – 0,95 = 0,05.

По таблице распределения Стьюдента находим значение t_gt = 2,0.

Тогда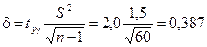

Доверительный интервал для неизвестного математического ожидания с надежностью g= 0,95равен: 29, 613 < m < 30,387.

Дата добавления: 2014-11-24; просмотров: 348; Нарушение авторских прав

Мы поможем в написании ваших работ!