Доверительные нтервалы для среднего квадратичного отклонения и дисперсии

При определении границ доверительных интервалов для дисперсии и среднего квадратического отклонения нормально распределенной случайной величины Х используется статистика 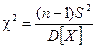, которая распределена по закону c²с n – 1 степенями свободы.

По заданной надежности g можно найти сколько угодно границ c²₁ и c²₂ интервалов, таких, что

Р (c²₁ < c²< c²₂) = g. (9.13)

При этом границы находятся из условий

Р (c² £ c²₁) = (1 – g)/2. (9.14)

Р (c² ³ c²₂) = (1 – g)/2. (9.15)

Для того, чтобы можно было воспользоваться таблицами распределения Пирсона (несимметричное распределение), преобразуем (9.14) в :

Р (c² ³ c²₁) = (1 + g)/2. (9.16)

Т.о. для нахождения доверительного интервала для дисперсии, значения концов интервала равны

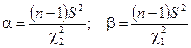. (9.17)

Пример 9.5. По данным выборки объема n = 26 из генеральной совокупности определена несмещенная оценка дисперсии S² = 4. Предполагая, что исследуемый количественный признак распределен нормально, найти доверительный интервал, накрывающий дисперсию D[X] с надежностью g = 0,95.

Решение. Для (1 + g)/2 = 0,975 и (1 – g)/2 = 0,025 при n – 1 = 25 по таблицам находим величины c²₁ = 13,12 и c²₂ = 40,65.

Вычисляем границы доверительного интервала

,

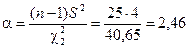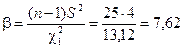
Значит, с надежностью 0,95 можно утверждать, что неизвестное значение дисперсии находится в границах: 2,46 < D[X] < 7,62.

При нахождении доверительного интервала для среднего квадратического отклонения s, исходя из определения доверительного интервала

Р (S – d < s < S + d) = g, (9.18)

для нахождения границ интервала необходимо знать закон распределения статистики, которая для этого случая преобразуется в .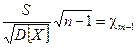

Тогда

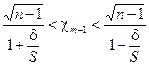. (9.19)

По заданным n и g по таблицам находим величину q = d/S.

Границы доверительного интервала

a = S (1 – q); b = S(1 + q). (9.20)

Пример 9.6. По данным выборки объема n = 26 из генеральной совокупности определена оценка средеквадратического отклонения ÖS² = 2. Предполагая, что исследуемый количественный признак распределен нормально, найти доверительный интервал, накрывающий sс надежностью g = 0,95.

Решение. По таблицам для g = 0,95 и n – 1 = 25 находим q = 0,32. Тогда по (9.20)

a = 2(1 – 0,32) = 1,36; b = 2 (1 + 0,32) = 2,64.

Значит, с надежностью 0,95 можно утверждать, что неизвестное значение среднеквадратического отклонения находится в границах:

1,36 < s < 2,64.

Дата добавления: 2014-11-24; просмотров: 388; Нарушение авторских прав

Мы поможем в написании ваших работ!