
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Статистические гипотезы
Статистической гипотезой называется любое предположение о виде закона распределения и (или) его параметрах. Статистические гипотезы делятся на непараметрические (о законе распределения) и параметрические (о его параметрах).
Например, статистической является гипотеза о том, что распределение производительности труда рабочих, выполняющих одинаковую работу в одинаковых условиях, имеет нормальный закон распределения. Статистической будет также гипотеза о том, что средние размеры деталей, производимые на однотипных, параллельно работающих станках, не различаются. Часто распределение величины X известно, и по выборке наблюдений необходимо проверить предположения о значении параметров этого распределения. Такие гипотезы называются параметрическими.
Статистическая гипотеза называется простой, если она однозначно определяет распределение случайной величины X, в противном случае гипотеза называется сложной. Например, простой гипотезой является предположение о том, что случайная величина X распределена по нормальному закону с математическим ожиданием, равным нулю, и дисперсией, равной единице. Если высказывается предположение, что случайная величина X имеет нормальное распределение с дисперсией, равной единице, а математическое ожидание — число из отрезка [a, b], то это сложная гипотеза.
Одну из гипотез выделяют в качестве основной (или нулевой) и обозначается H0. Наряду с гипотезой H0. рассматривают одну из альтернативных (конкурирующих) гипотез H1. Например, если проверяется гипотеза о равенстве параметра Q некоторому заданному значению Q0, то есть H0 : Q = Q0, то в качестве альтернативной гипотезы можно рассмотреть одну из следующих гипотез: H0(1) : Q > Q0 ; H0(2) : Q < Q0 ; H0(3) : Q ¹ Q0 ; H0(4) : Q = Q1 ; где Q1 — заданное значение, Q1 ¹ Q0. Выбор альтернативной гипотезы определяется конкретной формулировкой задачи.
Имея две гипотезы H0 и H1, на основе выборки прижимают либо основную, либо конкурирующую. Правило, по которому принимается решение принять или отклонить гипотезу H0, называется статистическим критерием (или просто критерием) проверки гипотезы H0.
Статистический критерий – это правило, по которому принимается решение по нулевой гипотезе. Для построения критерия выбирают статистику К, т. е. некоторую функцию от результатов измерений или наблюдений, находят (или заранее знают) ее распределение и (при традиционном подходе к применению статистических критериев) задаются некоторым ее значением, kкр вероятность превышения (или вероятность принятия меньшего значения) которого считается пренебрежимо малой и равной a.
Критическими точками (значениями) называют точки, отделяющие область принятия гипотезы от критической области. Критической областью называют совокупность значений статистики, при которых нулевая гипотеза отвергается.
Областью принятия гипотезы называется совокупность значений статистики, при которых гипотезу не отвергают. Если наблюденное значение статистики принадлежит критической области – гипотезу отвергают. Если значение статистики «попало» в область допустимых значений, то гипотезу не отвергают.
Т.е. могут быть допущены ошибки двух родов. Ошибка первого рода состоит в том, что отвергается нулевая гипотеза, когда она на самом деле верна. Ошибка второго рода – отвергается альтернативная гипотеза, когда она на самом деле верна. Вероятность ошибки первого рода (обозначается через a) называется уровнем значимости критерия. Уровень значимости a определяет размер критической области. Он задается обычно заранее. Чем меньше a, тем меньше вероятность отклонить верную гипотезу. Вероятность ошибки второго рода обозначают b. Вероятность b зависит от конкурирующей гипотезы и может быть вычислена только, если она является простой. Величина 1 – b называется мощностью критерия. Чем выше мощность критерия, тем он эффективнее. Чем меньше вероятность ошибки 1-го рода, тем больше вероятность ошибки 2-го рода.
Современный подход к применению статистических критериев состоит в том, что уровень значимости не задают заранее, а определяют по наблюденному значению статистики примененного критерия. Если этот уровень превышает 0,1, то принято считать, что нулевая гипотеза почти наверняка верна. Если этот уровень равен 0,01 или менее, то принято считать, что нулевая гипотеза почти наверняка неверна (в этом случае вероятность того, что она правильна всего лишь 1% или менее). Область значений a между 0,01 и 0,1 представляет собой область сомнений, когда желательно повторение опыта. Понятно, что оснований для сомнений тем больше, чем меньше a. Значение a = 0,05 считается таким, когда шансы отвергнуть правильную гипотезу (отвергнуть Н0, когда она верна) или принять неверную гипотезу (не отвергнуть Н0, когда она неверна) приблизительно равны.
Приложения

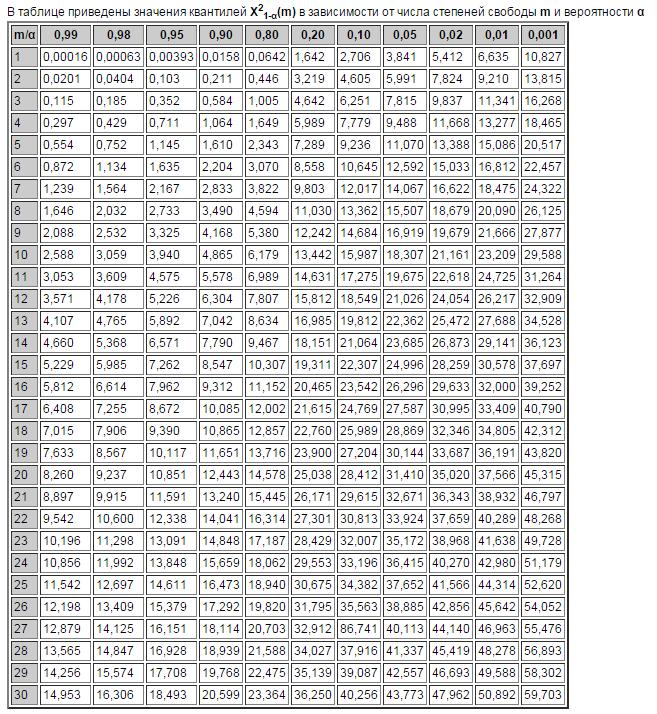
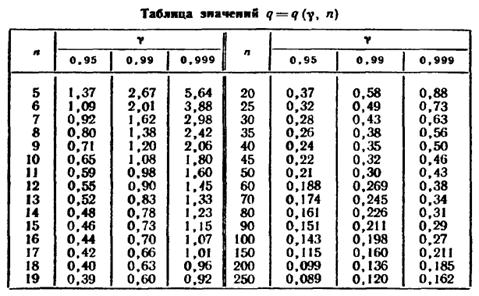
| <== предыдущая страница | | | следующая страница ==> |
| Доверительные нтервалы для среднего квадратичного отклонения и дисперсии | | |
Дата добавления: 2014-11-24; просмотров: 432; Нарушение авторских прав

Мы поможем в написании ваших работ!