
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Основные законы механики
ФИЗИКА
ЛЕКЦИЯ
по учебной дисциплине «ФИЗИКА»
Специальность 280705.65 - Пожарная безопасность
Заочное отделение
Раздел № 1 «Физические основы механики»
Обсуждена на заседании ПМС
Протокол №7
от «13» января 2012 г.
Санкт- Петербург
I. Цели занятия
1. Образовательная – изучение понятий и законов механики
2. воспитательные
- их применение в пожарной безопасности
- повышение квалификации сотрудников ГПС
II. Расчёт учебного времени
| Содержание и порядок проведения занятия | Время, мин. |
| ВВОДНАЯ ЧАСТЬ ОСНОВНАЯ ЧАСТЬ Учебные вопросы: 1. Основные понятия и определения механики 2. Основные законы механики ЗАКЛЮЧИТЕЛЬНАЯ ЧАСТЬ |
III. Литература
Основная:
1. Скребов В.Н., Трубилко А.И. Курс общей физики. Т. 1. Механика. — СПб: СПбУ ГПС МЧС России, 2011.
2. Трофимова Т.И. Курс физики. - М.: Высшая школа, 2009, с.6-14.
Компьютерные демонстрации:
1. Траектория движения.
2. Законы сложения скоростей.
3. Неравномерное движение.
4. Равномерное движение.
5. Равноускоренное движение.
6. Движение тела брошенного под углом к горизонту.
IV. Учебно-материальное обеспечение
- Технические средства обучения: мультимедийный проектор, интерактивная доска.
V. Текст лекции
Учебные вопросы
1 Основные понятия и определения механики
Предмет изучения механики – простейшие формы движения тел относительно друг друга, следовательно, необходимо в любой момент времени t знать местоположение материального тела.
Модели, их роль в познании природы: модель - условная замена реального объекта или явления, несет лишь существенные свойства, второстепенные – не учитывает. Модель – не копия, а лишь приближение к реальному процессу или объекту.
абсолютно твердое тело - также модель (условное понятие) в кинематике, размеры и форма которого неизменны при движении тела, т.е. тело не подвержено деформации;
материальная точка (система материальных точек) - формой, размерами и массой реального объекта можно пренебречь в рамках решаемой задачи движения тел;
движение тел – изменение телом своего положения в пространстве;
две составляющих движения тела: поступательное и вращательное;
поступательное движение - любая прямая, жестко связанная с телом, остается параллельной своему первоначальному положению. (Например, линия, проходящая вдоль бамперов пожарной автоцистерны);
возвратно-поступательное движение – разновидность поступательного движения (характерно для двигателей внутреннего сгорания и поршневых насосов пожарных автоцистерн). Тело периодически перемещается из одного положения в другое;
вращательное движение - все точки тела движутся по окружностям, центры которых лежат на одной прямой - оси вращения (центробежное колесо пожарных насосов автоцистерн, коленчатый вал д.в.с.);
одновременное наличие двух видов движения (колесо ЦН, колесо движущегося автомобиля имеют возможность не только вращаться вокруг оси, но и перемещаться вдоль оси вала, если изношен узел крепления колеса "шпонка-паз" вала вращения);
траектория движения - линия в пространстве, вдоль которой движется материальная точка (либо двигалась ранее, либо запланировано движение, например, ракеты);
путь (DS) - некоторая часть траектории, пройденная за время Dt;
перемещение - приращение радиус-вектора за рассматриваемый промежуток времени;
система координат - способ описания положения тел в пространстве: прямоугольная; цилиндрическая; сферическая.
Наиболее употребительна правая декартовая прямоугольная система координат. Способ задания положения материальной точки (М) в пространстве для некоторого момента времени х(t), у(t), z(t). Для начального положения х(0), у(0), z(0), т.е. М [х(0), у(0),z(0)];
система отсчета - тело отсчета, система координат и способ измерения времени;
скалярные и векторные значения скорости и ускорения:
а) скалярные величины - их выражают положительными или отрицательными числами без указания положения в пространстве (работа, мощность, масса);
б) векторные величины - их определяют не только размерами, но и направлением в пространстве (скорость, ускорение);
в) вектор - отрезок, имеющий определенную длину и направление;
векторное определение положения материальной точки: r = r(t) вместо скалярных величин х(t), y(t), z(t).
скорость движения – быстрота перемещения (по направлению и величине !!!) тела относительно других тел;
средняя скорость v ср или 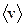 ;
;
v ср = DS/Dt, где DS и Dt - любые соответствующие друг другу значения (конечные разности), откуда DS I = VI . Dt I – площадь приближенно равна пройденному пути за Dt I ;
мгновенная скорость (v)
v = lim (DS/Dt) = dS/dt = d r/dt , при Dt 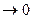 ;
;
ускорение движения – быстрота изменения скорости движения тела;
среднее ускорение (a ср или 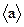 );
);
a ср = DV/Dt при Dt  0, где DV и Dt - любые соответствующие друг другу значения (конечные разности). По аналогии c пройденным путем имеем: V I = a I . Dt I;
0, где DV и Dt - любые соответствующие друг другу значения (конечные разности). По аналогии c пройденным путем имеем: V I = a I . Dt I;
мгновенное ускорение a = lim (Dv/Dt) = d2S/dt2; при Dt  0.
0.
Основные законы механики
2.1 Кинематика поступательного движения тел
Виды поступательного движения тел: прямолинейное, криволинейное, равномерное и неравномерное.
Основные уравнения кинематики поступательного движения
Поскольку в общем случае Dr = DS (где Dr = r2 - r1), то по аналогии со скалярной формой, можно записать:
v = lim(Dr/Dt) = dr/dt – мгновенная скорость;
a = lim (Dvср/Dt) = dv/dt = d2r/dt2 - мгновенное ускорение;
Уравнения (v =dr/dt; a =d2r/dt2) называют кинематическими уравнениями движения материальной точки;
Обобщённые координаты, независимые между собой параметры qi (r = 1, 2,..., s) любой размерности, число которых равно числу s степеней свободы механической системы и которые однозначно определяют положение системы. Закон движения системы в обобщенных координатах даётся s уравнениями вида qi = qi (t), где t — время.
Обобщённые координаты используются при решении многих задач, особенно когда система подчинена связям, налагающим ограничения на её движение. При этом значительно уменьшается число уравнений, описывающих движение системы, по сравнению, например, с уравнениями в декартовых координатах.
Интегрируя уравнения a = dv/dt, v = dS/dt (в пределах от 0 до t), получим:
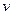 =
= 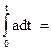
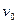 +
+ 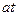 ; S=
; S= 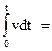
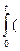
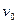 +
+ 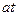 ) dt =
) dt = 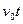 +
+ 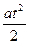 ;
;
Горизонтальная и вертикальная составляющие поступательного движения
Изобразим участок траектории 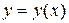 , где вектор элементарного перемещения
, где вектор элементарного перемещения 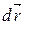 направлен под углом
направлен под углом 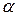 к оси
к оси 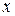 ; откуда получим: dx = r cos
; откуда получим: dx = r cos 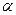 ; dу = r sin
; dу = r sin 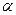 ;
;
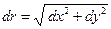 . Разделив dx и dу на
. Разделив dx и dу на 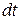 , найдем
, найдем
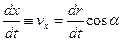 .
. 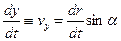 , где
, где 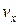 и
и 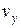 - величины вектора скорости по осям
- величины вектора скорости по осям 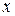 и
и 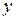 . Очевидно, что
. Очевидно, что 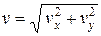 . Для пространственного случая
. Для пространственного случая 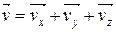 и тогда
и тогда 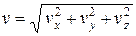 . Поскольку
. Поскольку 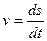 , то dSx=
, то dSx= 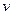 x . dt.
x . dt.
Из изложенного выше ( 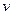 =
= 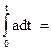
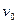 +
+ 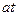 ; S=
; S= 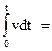
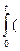
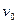 +
+ 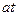 ) dt =
) dt = 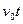 +
+ 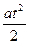 ) следует, что:
) следует, что: 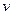
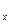 =
= 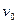
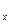 +
+ 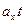 ; S
; S 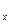 =
= 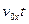 +
+ 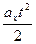 . Аналогично можно записать для вертикальной оси координат:
. Аналогично можно записать для вертикальной оси координат: 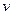 у =
у = 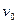 у +
у + 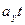 ; S
; S 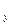 =
= 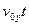 +
+ 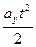 .
.
2.1.1 Кинематика криволинейного движения тел
При криволинейном движениив момент времени t тело находилось в точке А и имело линейную скорость 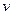 . Через
. Через 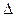 t оно оказалось в точке В, т.е. вектор линейной скорости изменил свое первоначальное положение, пройдя путь, равный
t оно оказалось в точке В, т.е. вектор линейной скорости изменил свое первоначальное положение, пройдя путь, равный 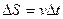 . При этом она повернулось на угол
. При этом она повернулось на угол 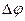 , равный
, равный 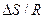 , или
, или  /R. Действуя по правилам сложения и разложения векторных величин, получим график, где
/R. Действуя по правилам сложения и разложения векторных величин, получим график, где 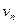 - нормальная составляющая,
- нормальная составляющая, 
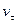 - касательная (тангенциальная) составляющие линейной скорости:
- касательная (тангенциальная) составляющие линейной скорости:
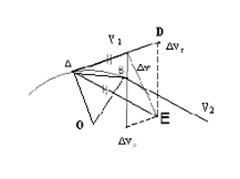 ОА = R
ОА = R 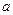 , ОВ = RВ – радиусы кривизны траекторий в точках А и В. Поскольку
, ОВ = RВ – радиусы кривизны траекторий в точках А и В. Поскольку 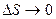 , то ОА = ОВ = R. Из подобия треугольников АОВ и ЕАD (взаимно перпендикулярные стороны) следует:
, то ОА = ОВ = R. Из подобия треугольников АОВ и ЕАD (взаимно перпендикулярные стороны) следует: 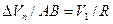 . Поскольку длина хорды АВ =
. Поскольку длина хорды АВ = 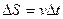 , то предыдущее соотношение сведется к виду:
, то предыдущее соотношение сведется к виду: 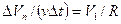 . Из него следует:
. Из него следует:
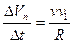 . При
. При 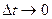 , имеем
, имеем 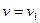 , и поскольку
, и поскольку 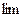
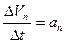 , то
, то 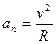 .
.
 нормальная составляющая ускорения, направлена по нормали к траектории, называют также - центростремительным ускорением.
нормальная составляющая ускорения, направлена по нормали к траектории, называют также - центростремительным ускорением. 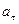 - тангенциальное ускорение. Полное ускорение
- тангенциальное ускорение. Полное ускорение
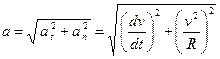 .
.
В зависимости от величин нормального и тангенциального ускорений, движение точки(тела) можно классифицировать на (целесообразно использовать слайд):1- прямолинейное равномерное ( 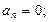
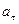 =0,
=0, 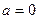 ), 2-прямолинейное неравномерное (
), 2-прямолинейное неравномерное ( 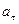 =
= 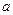 =
= 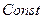 ,
, 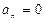 ), 3- прямолинейное с переменным ускорением (
), 3- прямолинейное с переменным ускорением ( 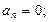
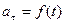 ) и т.д. (см. Трофимова, п.3)
) и т.д. (см. Трофимова, п.3)
2.1.2 Кинематика вращательного движения тел
При вращательном движении все точки тела движутся по окружностям, центры которых лежат на одной прямой - оси вращения. При переходе из положения 1 в 2 за время 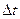 точка переместится на угол
точка переместится на угол 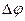 . Отношение
. Отношение 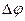 /
/ 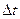 =
= 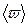 - средняя угловая скорость, lim (
- средняя угловая скорость, lim ( 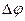 /
/ 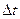 ) =
) = 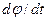 =
= 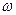 - мгновенная угловая скорость, псевдовектор которой – коаксиален, совпадает с направлением вращения правого винта (буравчика), может быть приложен в любой точке на оси вращения.
- мгновенная угловая скорость, псевдовектор которой – коаксиален, совпадает с направлением вращения правого винта (буравчика), может быть приложен в любой точке на оси вращения.
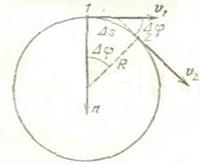 Длина пути (дуги)
Длина пути (дуги) 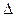 S=R
S=R 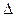 j (из синуса малых углов). Разделив на
j (из синуса малых углов). Разделив на 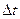 , получим
, получим 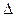 S/
S/ 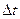 = R
= R 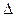 j /
j / 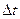 или
или 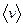 = R
= R 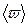 , для dt
, для dt 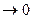 : мгновенное значение линейной скорости точки
: мгновенное значение линейной скорости точки 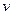 = Rw. Разделив его на
= Rw. Разделив его на 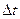 , получим соотношение
, получим соотношение 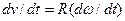 , т.е. между касательным (тангенциальным) ускорением
, т.е. между касательным (тангенциальным) ускорением 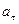 линейной скорости и ускорением e вращательного движения имеется связь:
линейной скорости и ускорением e вращательного движения имеется связь: 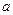
 = Re. Из рассмотрения криволинейного движения следует, что
= Re. Из рассмотрения криволинейного движения следует, что 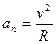 . Учтя, что
. Учтя, что 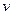 = Rw, получим
= Rw, получим 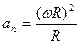 =
= 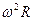 . Общность кинематики поступательного и вращательного движений можно проследить, пользуясь методом аналогий:
. Общность кинематики поступательного и вращательного движений можно проследить, пользуясь методом аналогий:
длина пути S 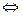 угол поворота j;
угол поворота j;
линейная скорость v = S/t 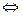
 угловая скорость w = j/t , их связь v = Rw;
угловая скорость w = j/t , их связь v = Rw;
линейное ускорение a = v/t 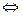 угловое ускорение e = w/t, их связь: a
угловое ускорение e = w/t, их связь: a  = Re. an = Rw2.
= Re. an = Rw2.
-для равномерного вращения w = 2pn, T = 2p/w, где n - число оборотов в единицу времени;
-правило правого винта для определения направления векторов w и e.
Типичная задача кинематики поступательного движения - определение дальности полета тел (например, гранаты и снаряда с огнетушащим веществом или струи воды), вылетающих из устройств под некоторым углом к горизонту. При таком движении, помимо горизонтальных составляющих, появляются вертикальные составляющие.
Воспользуемся ранее рассмотренными уравнениями:
S = vot + at2/2; Sх = vохt = vоt cosa; Sу = vоуt - gt2/2 ;
v = vo + at ; vox = voсosa; voу = vоsina;
из начального условия Sуо = 0, имеем:
vоуt = gt2/2 = 0; откуда t = 2vоу/g .
тогда Sx = vox(2voy/g). Окончательно дальность полета Sx = (2vo2 sina cosa)/g.
| <== предыдущая страница | | | следующая страница ==> |
| ПОСТРОЕНИЕ ЭВОЛЬВЕНТНЫХ ПРОФИЛЕЙ ЗУБЦОВ МЕТОДОМ ОБКАТКИ (ОГИБАНИЯ) | | | Уравнения динамики поступательного движения |
Дата добавления: 2014-11-24; просмотров: 279; Нарушение авторских прав

Мы поможем в написании ваших работ!