
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Векторная алгебра
1) Если даны точки 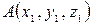 и
и 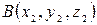 , то
, то 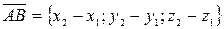 или
или 
2) Пусть 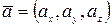 ,
, 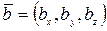 и
и 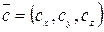 ,
, 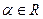 . Тогда
. Тогда
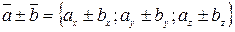 ,
,  .
.
3) Условие коллинеарности векторов: 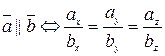 .
.
4) Модуль (длина) вектора: 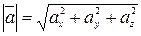 .
.
5) Направляющие косинусы
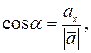
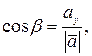
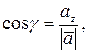 причем
причем 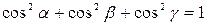 ,
,
 - орт вектора
- орт вектора 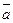
6) Скалярное произведение векторов: 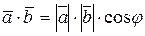 или
или 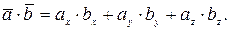
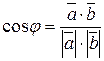 ;
; 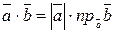 ;
; 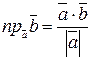 .
.
7) Условие перпендикулярности векторов: 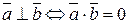 .
.
8) Векторное произведение векторов: 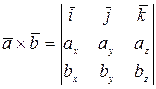 .
.
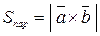 ;
; 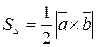 .
.
9) Смешанное произведение векторов: 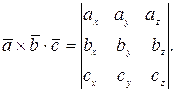
Если 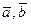 и
и 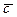 компланарны, то
компланарны, то 
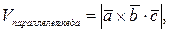
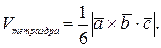
10) Деление отрезка в данном отношении:
Если 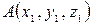 и
и 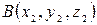 - концы отрезка, а
- концы отрезка, а 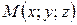 - точка, делящая отрезок в отношении
- точка, делящая отрезок в отношении 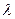 , то
, то 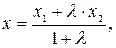
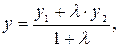
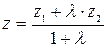 .
.
Прямая на плоскости
1) 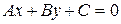 - общее уравнение прямой;
- общее уравнение прямой;
2) 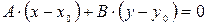 - уравнение прямой, проходящей через точку
- уравнение прямой, проходящей через точку 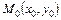 перпендикулярно вектору
перпендикулярно вектору 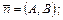
3) 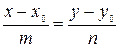 - каноническое уравнение прямой, проходящей через точку
- каноническое уравнение прямой, проходящей через точку 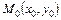 параллельно направляющему вектору
параллельно направляющему вектору 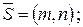
4) 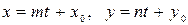 -параметрические уравнения прямой;
-параметрические уравнения прямой;
5) 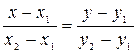 - уравнение прямой, проходящей через две точки
- уравнение прямой, проходящей через две точки 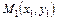 и
и 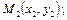
6) 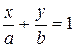 - уравнение прямой в отрезках, где
- уравнение прямой в отрезках, где 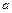 и
и 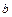 - величины отрезков, отсекаемых прямой на координатных осях
- величины отрезков, отсекаемых прямой на координатных осях 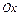 и
и 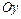 соответственно;
соответственно;
7) 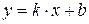 - уравнение прямой с угловым коэффициентом, где
- уравнение прямой с угловым коэффициентом, где 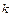 - угловой коэффициент прямой, а
- угловой коэффициент прямой, а 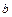 - отрезок, отсекаемый прямой на оси
- отрезок, отсекаемый прямой на оси 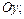
8) 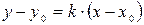 - уравнение прямой, проходящей через точку
- уравнение прямой, проходящей через точку 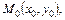 где
где 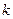 - угловой коэффициент прямой.
- угловой коэффициент прямой.
9) Угол 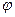 между двумя прямыми
между двумя прямыми 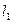 и
и 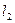 :
: 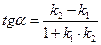 и
и 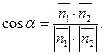
10) Условие перпендикулярности: 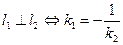 или
или 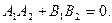
11) Условие параллельности: 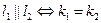 или
или 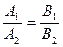 .
.
12) Расстояние от точки 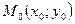 до прямой
до прямой 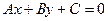 :
:
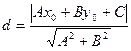 .
.
Кривые второго порядка
1) Каноническое уравнение окружности: 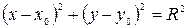
центр в точке 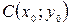 радиус равен
радиус равен 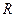 .
.
2) Каноническое уравнение эллипса: 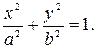
Числа 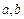 называются полуосями эллипса, точки
называются полуосями эллипса, точки 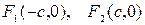 - фокусы эллипса,
- фокусы эллипса,
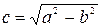 .
.
Отношение 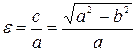 называется эксцентриситетом эллипса.
называется эксцентриситетом эллипса.
3) Каноническое уравнение гиперболы 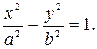
Числа 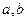 называются действительной и мнимой полуосями, точки
называются действительной и мнимой полуосями, точки 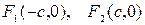 -фокусы гиперболы,
-фокусы гиперболы, 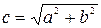 .
.
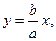
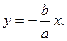 -асимптоты гиперболы.
-асимптоты гиперболы.
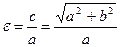 - называется эксцентриситетом гиперболы.
- называется эксцентриситетом гиперболы.
4) Каноническое уравнения параболы: 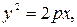
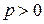
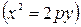
Точка 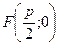 - фокус параболы
- фокус параболы 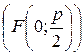 .
.
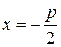 - уравнение директрисы параболы
- уравнение директрисы параболы 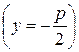 .
.
Плоскость
1) 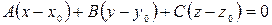 - уравнение плоскости, проходящей через точку
- уравнение плоскости, проходящей через точку 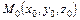 перпендикулярно вектору
перпендикулярно вектору  ;
;
2) 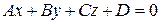 - общее уравнение плоскости
- общее уравнение плоскости  - нормаль плоскости;
- нормаль плоскости;
3) 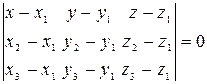 - уравнение плоскости, проходящей через три заданные точки
- уравнение плоскости, проходящей через три заданные точки 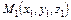 ,
, 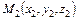 и
и 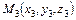 ;
;
4) 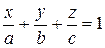 - уравнение плоскости в отрезках, где
- уравнение плоскости в отрезках, где 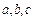 - величины направленных отрезков, отсекаемых плоскостью на координатных осях
- величины направленных отрезков, отсекаемых плоскостью на координатных осях 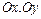 и
и 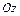 соответственно.
соответственно.
5) Угол 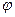 между двумя плоскостями:
между двумя плоскостями:
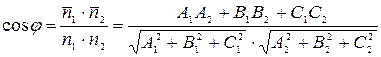 .
.
6) Условие параллельности двух плоскостей: 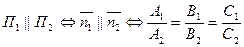 .
.
7) Условие перпендикулярности двух плоскостей:
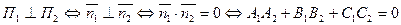 .
.
8) Расстояние от точки 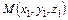 до плоскости
до плоскости 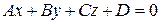 находят по формуле
находят по формуле
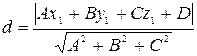
Прямая в пространстве
1)  - канонические уравнения прямой в пространстве, проходящей через точку
- канонические уравнения прямой в пространстве, проходящей через точку 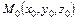 параллельно вектору
параллельно вектору 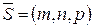 ;
;
2) 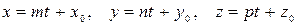 -параметрические уравнения;
-параметрические уравнения;
3) 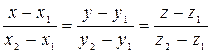 - уравнения прямой в пространстве, проходящей через две точки
- уравнения прямой в пространстве, проходящей через две точки 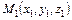 ,
, 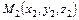 ;
;
4) 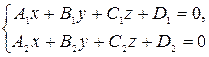 - общие уравнения прямой.
- общие уравнения прямой.
Направляющий вектор этой прямой 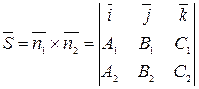 .
.
5) Угол между двумя прямыми 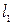 и
и 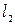 :
:
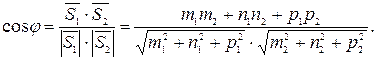
6) Условие параллельности двух прямых: 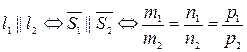 .
.
7) Условие перпендикулярности двух прямых: 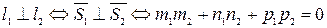 .
.
8) Угол между прямой и плоскостью: 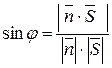 .
.
9) Условие параллельности прямой и плоскости: 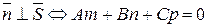 .
.
10) Условие перпендикулярности прямой и плоскости: 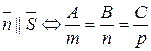 .
.
| <== предыдущая страница | | | следующая страница ==> |
| Основные положения теории базирования | | | Основы аудиторской деятельности в РФ |
Дата добавления: 2014-11-24; просмотров: 316; Нарушение авторских прав

Мы поможем в написании ваших работ!