Алгебра событий. Суммой событий А и В называется событие А+В, которое заключается в том, что происходит хотя бы одно из этих событий

Суммой событий А и В называется событие А+В, которое заключается в том, что происходит хотя бы одно из этих событий.

Произведением событий А и В называется событие А×В, которое заключается в том, что происходят оба этих события. Если А×В – невозможное событие, то события А и В называются несовместными.

Разностью между событием А и событием В называется событие А–В, которое заключается в том, что событие А происходит, а событие В не происходит.

Событием, противоположным событию А, называется событие`А, которое заключается в том, что событие А не происходит.

Задача 4. Докажите, что А – В = А ×`В; `А = W – А.

Поскольку для нас события – это подмножества пространства W, то суммой двух событий будет объединение соответствующих множеств, а произведением – пересечение этих множеств. Разность событий – это разность множеств, а противоположное событие – это дополнение множества А до пространства W. То есть речь у нас фактически идет не о введении новых понятий (операций над событиями), а о введении новой терминологии. Это введение оправдано тем, что, во-первых, новая терминология отвечает исторической традиции, а, во-вторых, она лучше позволяет осознать специфику ситуации. Так, фразы «событие А влечет событие В» и «множество А содержится во множестве В» означают одно и то же, однако первая все же несет некую дополнительную информацию – речь, дескать, идет не просто о множествах, а о подмножествах некоторого пространства элементарных исходов…

Но так как все-таки операции над событиями есть обыкновенные теоретико-множественные операции, то для них справедливы все свойства этих операций.

Задача 5. Докажите, что A×(B+C) = A×B+A×C; .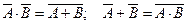

Задача 6. Антон, Борис и Сергей сдают экзамен. Событие А заключается в том, что Антон получил пятерку, В – Борис получил пятерку, С – Сергей получил пятерку. Задайте с помощью операций умножения, сложения и перехода к противоположному событию следующие события:

а) мальчики получили ровно 1 пятерку;

б) мальчики получили ровно 2 пятерки;

в) мальчики получили не менее двух пятерок;

г) мальчики получили не более 1 пятерки;

д) Борис и еще один из мальчиков получили пятерки.

Что в данной ситуации является пространством элементарных исходов? Сколько в нем элементов? Сколько исходов благоприятствуют каждому из приведенных выше событий?

Дата добавления: 2014-11-15; просмотров: 270; Нарушение авторских прав

Мы поможем в написании ваших работ!