
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Вероятностное пространство
Пусть 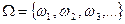 – пространство элементарных исходов. Вероятностью на пространстве W называется заданная на этом пространстве числовая функция Р, обладающая двумя свойствами:
– пространство элементарных исходов. Вероятностью на пространстве W называется заданная на этом пространстве числовая функция Р, обладающая двумя свойствами:
1) Р(wi) ³ 0 для всех i;
2) Р(w1) + Р(w2) + Р(w3) + … = 1
Величину Р(wi) называют вероятностью исхода wi и обозначают рi. Эта величина характеризует частоту появления данного исхода в результате проведения серии экспериментов.
Вероятность на пространстве W удобно бывает задавать с помощью таблицы:
| w1 | w2 | w3 | … |
| р1 | р2 | р3 | … |
Такая таблица иногда называется распределением вероятности на пространстве W.
Задача 7. Пространство W состоит из 4 исходов, вероятности которых пропорциональны числам 1, 2, 3 и 4. Определить эти вероятности.
Пространство элементарных исходов W с заданной на нем вероятностью Р называется вероятностным пространством.
Вероятностью события А называется сумма вероятностей элементарных исходов, благоприятствующих этому событию: 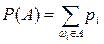 . При этом вероятность невозможного события полагается равной нулю.
. При этом вероятность невозможного события полагается равной нулю.
Задача 8. Пусть 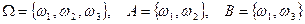 . Известно, что Р(А) = 0,8; Р(В) = 0,6. Найти вероятности всех элементарных исходов.
. Известно, что Р(А) = 0,8; Р(В) = 0,6. Найти вероятности всех элементарных исходов.
Свойства вероятности.
1.Р(W) = 1
2.0£Р(А)£1 для любого события А
3.Если АÌВ, то Р(А)£Р(В)
4.Если события А и В несовместны, то Р(А+В) = Р(А) + Р(В)
5. Р(А+В) = Р(А) + Р(В) – Р(А×В) для любых событий А и В
6. 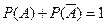 .
.
Центральное место среди этих свойств занимает, несомненно, свойство 4. Присмотритесь к нему внимательно и испытайте радость узнавания – это знакомое нам по комбинаторике свойство аддитивности (или правило сложения), только вместо количества элементов во множествах А и В здесь мы имеем дело с вероятностями соответствующих событий.
Задача 9. Докажите свойства 1 – 6.
Важный пример.
Пусть у нас имеется вероятностное пространство (W, Р), где 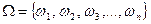 , а вероятность Р задана набором чисел {р1, р2, р3, … }. Известно, что в результате некоторого эксперимента произошло событие А =
, а вероятность Р задана набором чисел {р1, р2, р3, … }. Известно, что в результате некоторого эксперимента произошло событие А = 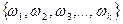 , однако не известно, какой именно элементарный исход имел место. Что можно сказать о вероятности исхода wi с учетом этой информации? Обозначим эту вероятность через pi(A). Понятно, что при i>k следует считать pi(A) = 0. При i£k числа pi(A) должны быть пропорциональны числам pi, то есть можно положить pi(A) = kpi. При этом должно выполняться условие p1(A)+p2(A)+p3(A)+…+pk(A) = 1, то есть k×(p1+p2+p3+…+pk) = 1. Но сумма, стоящая в скобках, – это вероятность события А. Таким образом k×p(A) = 1 и
, однако не известно, какой именно элементарный исход имел место. Что можно сказать о вероятности исхода wi с учетом этой информации? Обозначим эту вероятность через pi(A). Понятно, что при i>k следует считать pi(A) = 0. При i£k числа pi(A) должны быть пропорциональны числам pi, то есть можно положить pi(A) = kpi. При этом должно выполняться условие p1(A)+p2(A)+p3(A)+…+pk(A) = 1, то есть k×(p1+p2+p3+…+pk) = 1. Но сумма, стоящая в скобках, – это вероятность события А. Таким образом k×p(A) = 1 и 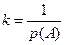 . Итак, мы построили новое вероятностное пространство, для которого пространством элементарных исходов является множество А, а вероятности элементарных исходов задаются формулами
. Итак, мы построили новое вероятностное пространство, для которого пространством элементарных исходов является множество А, а вероятности элементарных исходов задаются формулами 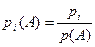 .
.
Задача 10. Как найти вероятность события В, если известно, что произошло событие А?
Решение. Вероятность события В (при условии, что произошло событие А) – это сумма тех pi(A), для которых 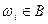 . Так как pi(A) отличны от нуля лишь тогда, когда
. Так как pi(A) отличны от нуля лишь тогда, когда 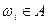 , то окончательно имеем, что искомая вероятность равна
, то окончательно имеем, что искомая вероятность равна 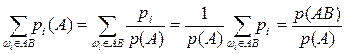 .
.
Найденная нами в задаче 9 величина носит название условной вероятности и обозначается p(BïA) (читается «вероятность B при условии A»). Таким образом имеем:
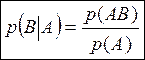 (1)
(1)
Обычно эта формула служит определением условной вероятности. Формулу (1) обычно используют для определения вероятности произведения двух (или нескольких) событий:
р(АВ) = р(А)×р(ВïА) (2)
Задача 11. Доказать, что если р(ВïА) = р(В), то р(АïВ) = р(А).
Результат этой задачи позволяет дать следующее определение:
События А и В называются независимыми, если р(АВ) = р(А)р(В).
Независимость двух событий означает, что вероятность каждого из них не зависит от того, произошло другое событие или нет, то есть р(ВïА) = р(В) и р(АïВ) = р(А).
Как определяют pi?
Для того, чтобы изложенная выше теория имела какое-то практическое применение, следует предложить разумный способ нахождения pi. Обычно для этого применяют два подхода. Классический подход заключается в том, что вероятности всех элементарных исходов считаются одинаковыми. Этот подход применим лишь в случае, когда пространство элементарных исходов конечно. Статистический подход предполагает проведение большого количества экспериментов, после чего в качестве pi берется частота исхода wi, то есть отношение числа экспериментов, при которых данный исход имел место, к общему количеству экспериментов.
Какой из двух подходов следует применить для решения данной задачи, обычно бывает понятно из ее условия. Так, при подбрасывании симметричного кубика все исходы следует считать равновероятными. Если же кубик имеет какой-либо дефект, то надо применить статистический подход.
Задача 12. Докажите, что при классическом определении вероятности справедлива формула
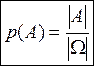 (3)
(3)
Формула (3) позволяет находить вероятность данного события чисто комбинаторными методами.
Задача 13. Из карточной колоды (36 карт) берется карта. Какова вероятность, что она бубновой масти?
Решение. В данном случае пространство W состоит из 36 элементарных исходов (по числу карт в колоде). Предположение о том, что эти исходы равновероятны, не выглядит слишком смелым. Так как благоприятных исходов 9, то, согласно формуле (3) 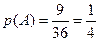 .
.
Задача 14. Из карточной колоды (36 карт) берутся две карты. Какова вероятность, что обе они бубновой масти?
Решение. Будем считать, что обе карты извлекаются из колоды одновременно. Тогда пространство элементарных исходов W состоит из неупорядоченных пар (то есть сочетаний из 36 по 2). Их общее количество 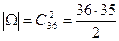 . Множество благоприятных исходов состоит из неупорядоченных пар карт бубновой масти. Их общее количество
. Множество благоприятных исходов состоит из неупорядоченных пар карт бубновой масти. Их общее количество 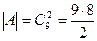 =36. Отсюда
=36. Отсюда 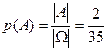 .
.
Этот результат не изменится, если считать, что карты извлекаются из колоды последовательно одна за другой. Только в этом случае вместо сочетаний нам придется рассмотреть размещения, в результате чего число исходов (как всех, так и благоприятных) возрастет в два раза.
Однако данную задачу можно решать совсем по-другому, основываясь на понятии условной вероятности. Будем считать, что карты извлекаются из колоды последовательно. Тогда событие А можно представить как произведение событий А1 (первая карта бубновой масти) и А2 (вторая карта бубновой масти). Из формулы (2) следует, что р(А) = р(А1)×р(А2ïА1) = 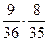 . Вычисляя условную вероятность р(А2ïА1) мы исходим из того, что при вытаскивании второй карты в колоде осталось только 35 карт, из них 8 бубен.
. Вычисляя условную вероятность р(А2ïА1) мы исходим из того, что при вытаскивании второй карты в колоде осталось только 35 карт, из них 8 бубен.
Задача 15. Из карточной колоды (36 карт) берутся две карты. Какова вероятность следующих событий:
1) А – выбрано ровно два короля;
2) В – выбран ровно один король;
3) С – не выбрано ни одного короля;
4) D – выбран хотя бы один король;
5) Е – выбран один король и одна дама, причем их масти не совпадают.
Задача 16. В коробке лежит три синих, четыре красных и пять черных шаров. Наугад извлекаются три шара. Какова вероятность, что все они одного цвета? Какова вероятность, что все три шара разных цветов?
Задача 17. 6 карточек с буквами М, О, Л, О, К и О в произвольном порядке выкладываются на стол. Какова вероятность, что при этом получится слово МОЛОКО? Какова вероятность, что две буквы О не окажутся рядом?
Задача 18. 12 команд произвольным образом разбиваются на две подгруппы по 6 команд в каждой. Какова вероятность, что две наиболее сильные команды окажутся в одной подгруппе?
Решение. Назовем две сильнейшие команды «Спартак» и ЦСКА. В качестве элементарного исхода будем рассматривать неупорядоченную выборку, состоящую из пяти команд, попавших в одну группу со «Спартаком». Тогда 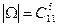 . Благоприятный исход – это такая выборка, в которой присутствует ЦСКА, остальные же 4 команды выбираются из 10 оставшихся. Таким образом, число благоприятных выборок равно
. Благоприятный исход – это такая выборка, в которой присутствует ЦСКА, остальные же 4 команды выбираются из 10 оставшихся. Таким образом, число благоприятных выборок равно 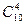 . То есть искомая вероятность равна
. То есть искомая вероятность равна 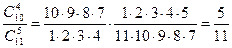 .
.
Задача 19. 12 команд произвольным образом разбиваются на три подгруппы по 4 команды в каждой. Какова вероятность, что три наиболее сильные команды окажутся в разных подгруппах?
Задача 20. Игральную кость бросают до тех пор, пока не выпадет шестерка. Какова вероятность, что это событие рано или поздно произойдет?
Решение. Вероятность того, что шестерка не выпадет ни разу за n бросаний равна 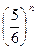 . Соответственно, вероятность того, что шестерка выпадет хотя бы раз (за n бросаний), равна
. Соответственно, вероятность того, что шестерка выпадет хотя бы раз (за n бросаний), равна 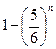 . Вероятность того, что шестерка выпадет когда-нибудь, не меньше этой величины. Так как с ростом n величина
. Вероятность того, что шестерка выпадет когда-нибудь, не меньше этой величины. Так как с ростом n величина 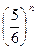 стремится к нулю, то искомая вероятность равна 1.
стремится к нулю, то искомая вероятность равна 1.
Задача 21. Сколько раз нужно бросить игральную кость, чтобы появление шестерки имело вероятность, большую 0,8?
Задача 22. Монету бросают до тех пор, пока два раза подряд не выпадет орел. Какова вероятность, что это событие рано или поздно произойдет?
Задача 23. Двое поочередно вынимают (без возвращения) шары из коробки, содержащей 4 черных и два белых шара. Побеждает тот, кто первым вытаскивает белый шар. Какова вероятность, что победителем окажется игрок, сделавший первый ход?
Задача 24. Пусть события А и В независимы. Докажите, что события А и 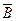 тоже независимы.
тоже независимы.
Задача 25. Пусть 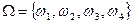 – пространство, состоящее из 4 равновероятных исходов;
– пространство, состоящее из 4 равновероятных исходов; 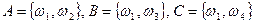 . Проверьте, что эти три события попарно независимы, в то же время равенство Р(АВС) = Р(А)Р(В)Р(С) не выполняется.
. Проверьте, что эти три события попарно независимы, в то же время равенство Р(АВС) = Р(А)Р(В)Р(С) не выполняется.
События А1, А2,…,Аn называются независимыми в совокупности, если для любой группы событий Аi вероятность произведения событий, входящих в эту группу, равна произведению их вероятностей.
Результат задачи 25 показывает, что попарно независимые события не обязаны быть независимыми в совокупности.
Формула полной вероятности
Задача 26. Докажите, что для любых событий А и В справедлива формула
P(A) = P(AôB)×P(B) + P(Aï 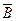 )×P(
)×P( 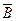 )
)
Указание. Воспользуйтесь равенством 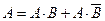 .
.
Задача 27. В 40% ящиков белые шары составляют 60%, а в 60% ящиков они составляют 20%. Из случайно взятого ящика наугад выбирается шар. Какова вероятность, что этот шар белый?
Решение. Пусть событие В состоит в том, что выбран ящик первого типа. Тогда Р(В) = 0,4; P( 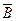 ) = 0,6; P(AôB) = 0,6; P(Aï
) = 0,6; P(AôB) = 0,6; P(Aï 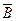 ) = 0,2. Применяя формулу из предыдущей задачи, получим Р(А) = 0,6×0,4+0,2×0,6 = 0,36.
) = 0,2. Применяя формулу из предыдущей задачи, получим Р(А) = 0,6×0,4+0,2×0,6 = 0,36.
Формулу из задачи 26 удобно применять в ситуации, когда последовательно проводятся два эксперимента, причем результат первого (произошло или не произошло событие В) существенно влияет на результат второго. Легко, однако, представить ситуацию, когда количество возможных исходов первого эксперимента гораздо больше двух.
Задача 28. Пусть события Н1, Н2,…Нn попарно несовместны и в сумме дают все пространство W. Тогда справедлива формула
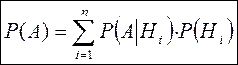 (4)
(4)
Эта формула называется формулой полной вероятности.
Задача 29. В физико-математическом классе учится 50% математиков, 30% физиков и 20% лодырей. Каждый из математиков выучили по 80% заданных учителем формул, каждый из физиков – по 60%, а каждый из лодырей – по 10%. Какова вероятность, что случайно выбранный ученик правильно напишет необходимую формулу? А если нужно написать две формулы, то с какой вероятностью ученик правильно напишет обе? Хотя бы одну?
Задача 30. Система может находиться в одном из трех состояний: А, В и С. В течение минуты она с вероятностью 0,4 совершает переход из состояния А в состояние В, с вероятностью 0,3 – в состояние С (и с вероятностью 0,3 продолжает оставаться в состоянии А). Переходы В®А, В®С и ® имеют вероятности 0,5; 0,2 и 0,3 соответственно, а переходы С®А, Ѯ и С®С происходят с вероятностью 0,1; 0,3 и 0,6 соответственно. В начальный момент времени система находилась в состоянии А. Какова вероятность, что через две минуты она будет находиться в состоянии А? В состоянии В? В состоянии С? А что можно сказать о состоянии системы через три минуты?
Задача 31. Если Вася подготовится к уроку с помощью репетитора, то он получит пятерку с вероятностью 0,9 (в том случае, конечно, если его вызовут к доске); если он подготовится к уроку сам, то получит пятерку с вероятностью 0,5; если же Вася не подготовится к уроку, то вероятность получить пятерку составит 0,1. Известно, что Вася занимается с репетитором один раз в неделю, три раза в неделю он ходит на секцию айкидо и потому в эти дни к занятиям не готовится, в оставшиеся два дня Вася учит уроки самостоятельно (в субботу вечером Вася отдыхает в кругу друзей). Если известно, что Васю за неделю спросили один раз, то какова вероятность, что он получил пятерку? А если Васю спросят дважды (в разные дни), то какова вероятность, что он получит две пятерки? А с какой вероятностью он может в этом случае рассчитывать хотя бы на одну пятерку?
Замечание. Для решения второй части этой задачи (Васю спрашивают дважды) следует очень аккуратно рассмотреть следующие ситуации: РС, РН, СС, СН, НН. Буквы Р, С и Н означают, что в тот день, когда Васю вызывали к доске, он, соответственно, готовился к уроку с репетитором, готовился сам, не готовился вообще. Необходимо определить, с какой вероятностью Вася попадает в каждую из этих пяти ситуаций. Если событие А означает, что Вася получил две пятерки, то далее мы должны найти пять условных вероятностей: Р(АôРС), Р(АôРН), Р(АôСС), Р(АôСН) и Р(АôНН). То же для события В, означающего, что Вася получил хотя бы одну пятерку. Например, Р(ВôРС) = 0,9+0,5–0,9×0,5 = 0,95. Действительно, событие В можно представить в виде суммы двух событий: В1 – пятерка получена в тот день, когда Вася занимался с репетитором и В2 – пятерка получена в тот день, когда Вася занимался сам. Далее мы пользуемся формулой Р(В1+В2)=Р(В1)+Р(В2)–Р(В1В2).
Задача 32. Известно, что у 50% курильщиков желтые зубы, а среди некурящих людей этот процент составляет 20%. Стоматологический осмотр, проведенный в 17 школе, показал, что 30% старшеклассников имеют желтые зубы. Каков (примерно) процент курильщиков среди учащихся старших классов 17 школы?
Замечание. В этой задаче известна вероятность события А (у ученика желтые зубы), но неизвестна вероятность события В (ученик курит). Чтобы найти эту вероятность, следует воспользоваться формулой из задачи 26 и соотношением P( 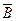 ) =1– Р(В).
) =1– Р(В).
Очень часто при последовательном проведении двух испытаний (экспериментов) нам бывает известен результат второго эксперимента (событие А произошло), и мы хотим сделать прогноз относительно результата первого эксперимента, то есть определить вероятность Р(HkôА).
Задача 33. Докажите справедливость следующей формулы:
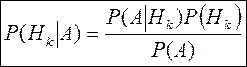 (5)
(5)
Задача 34. В 40% ящиков белые шары составляют 60%, а в 60% ящиков они составляют 20%. Из случайно взятого ящика наугад выбирается шар. Какова вероятность, что был взят ящик первого типа, если этот шар оказался белым?
При применении формулы (5) вероятность Р(А) обычно вычисляется с помощью формулы (4). Если соединить эти две формулы вместе, то получится формула, которая носит название формула Байеса:
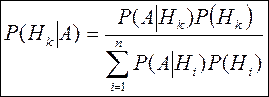 (6)
(6)
Задача 35. 20% выпускников 17 школы собираются поступать в московские вузы, 30% – в ТГТУ и 50% – в ТвГУ. Среди поступающих в московские вузы 20% сдают выпускной экзамен по ОБЖ, среди поступающих в ТГТУ и ТвГУ этот процент составляет 60% и 40% соответственно. Известно, что Вася решил сдавать экзамен по ОБЖ. Какова вероятность, что он собирается продолжить свое образование в ТГТУ?
Схема Бернулли.
Как уже говорилось ранее, вероятность р события А характеризует частоту, с которой происходит это событие при проведении достаточно большого количества экспериментов. При этом эксперименты должны проводиться в одинаковых условиях, и результаты разных экспериментов не должны зависеть друг от друга. В этом случае принято говорить о серии из n независимых испытаний или о схеме Бернулли с параметрами n и р.
Итак, пускай проводится n независимых испытаний. В результате одного испытания событие А происходит с вероятность р (и не происходит с вероятностью q = 1–p). Если в результате данного испытания событие А произошло, то это испытание будет называться успешным. Нас будет интересовать вопрос о количестве успешных испытаний в серии из n испытаний. Обозначим через Pn(m) вероятность того, что в серии из n независимых испытаний имело место ровно m успехов.
Задача 36. Докажите, что справедлива так называемая формула Бернулли:
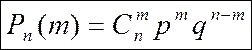 (7)
(7)
Решение. Результат серии испытаний можно записать как упорядоченный набор из нулей и единиц, в котором единица соответствует успешно проведенному испытанию, а нуль означает, что в соответствующем испытании событие А не произошло. Вероятность того, что на k-ом месте в этом наборе стоит единица равна р, нуль – q. Так как испытания независимы, то вероятность результата серии равна произведению вероятностей результатов отдельных испытаний. В этом произведении m раз встречается число р и n–m раз – число q. То есть вероятность результата серии, содержащей m успешных испытаний, равна pm×qn–m. Осталось сосчитать количество наборов, состоящих из m нулей и n–m единиц. Таких наборов, очевидно, 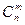 . Отсюда получаем справедливость формулы (7).
. Отсюда получаем справедливость формулы (7).
Задача 37. Какова вероятность, что при 10 бросаниях игральной кости шестерка выпадет ровно один раз? Ровно 2 раза?
Задача 38. Стрелок попадает в цель с вероятностью 0,2. Какова вероятность, что из десяти выстрелов он ровно 2 раза попадет в цель? Сколько выстрелов надо сделать, чтобы с вероятностью не менее 0,9 попасть в цель не менее двух раз?
Задача 39. Какое число успехов является наиболее вероятным в схеме Бернулли с параметрами n и р?
Указание. Решите неравенство 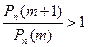 .
.
Приложение 2.
Контрольная работа по теории вероятностей (проводилась в 2001 году в 11б классе сш №17 г. Твери).
Вариант 1
1. Р(А)=0,6; Р(В)=0,4; Р(АВ)=0,2. Найти Р(А+В), 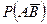 .
.
2. Вероятностное пространство состоит из 4 элементарных исходов: 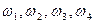 , вероятности которых пропорциональны числам 1, 2, 3 и 4.
, вероятности которых пропорциональны числам 1, 2, 3 и 4. 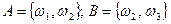 . Найти Р(А½В). Будут ли события А и В независимы?
. Найти Р(А½В). Будут ли события А и В независимы?
3. В 11б классе случайным образом выбирают одного мальчика и одну девочку для участия в игре «Счастливый случай». Какова вероятность, что это будут Саша и Настя? Какова вероятность, что среди них будет Лена или Олег? (В 11б классе 8 девочек и 17 мальчиков, из них 3 Насти, 2 Лены, 3 Саши и 3 Олега).
4. В коробке 10 красных и 6 синих шаров. Ваня достает 5 шаров. Какова вероятность, что он вытащит ровно 2 синих шара? Какова вероятность, что он вытащит хотя бы один синий шар?
5. Вероятность того, что богатая невеста имеет плохой характер, равна 0,8; бедная – 0,4. В Твери 20% богатых и 80% бедных невест. Ваня женился на первой встречной и, увы, ему досталась жена с плохим характером. Какова вероятность, что она богата?
6. Кубик кидают 4 раза. Какова вероятность, что ровно 2 раза выпадет шестерка?
Вариант 2
1. Р(А)=0,5; Р(В)=0,4; Р(А+В)=0,7. Найти Р(АВ), 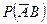 .
.
2. Вероятностное пространство состоит из 4 элементарных исходов: 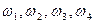 , вероятности которых пропорциональны числам 1, 2, 2 и 3.
, вероятности которых пропорциональны числам 1, 2, 2 и 3. 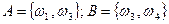 . Найти Р(А½В). Будут ли события А и В независимы?
. Найти Р(А½В). Будут ли события А и В независимы?
3. Василий Сергеевич случайным образом построил в шеренгу трех Антонов и трех Дим. Какова вероятность, Дима Сапожников и Антон Цуканов будут стоять рядом? Какова вероятность, что Антон Кошелев будет стоять с краю?
4. В коробке 2 красных и 3 синих шара. Двое ученых по очереди тащат шары, пока не вытащат красный. Какова вероятность, что первым это сделает первый ученый?
5. 2 раза в неделю Андрей Клишов готовит уроки. Если он идет в школу с выученными уроками, то вероятность получить пятерку равна 0,7; если с невыученными – то 0,2. Известно, что в субботу Андрей получил пятерку. Какова вероятность, что в этот день он выучил уроки?
6. Кубик кидают 10 раз. Какова вероятность, что шестерка выпадет хотя бы раз? Что она выпадет ровно 1 раз?
Вариант 3
1. Р(А)=0,6; Р(В)=0,4; А и В независимы. Найти Р(А+В), 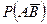 .
.
2. Вероятностное пространство состоит из 4 элементарных исходов: 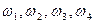 .
. 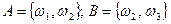 . Известно, что Р(w1)=0,4, Р(w3)=0,2, Р(А½В)=0,5. Найти Р(А) и Р(В).
. Известно, что Р(w1)=0,4, Р(w3)=0,2, Р(А½В)=0,5. Найти Р(А) и Р(В).
3. В 11б классе случайным образом выбирают двух мальчиков и двух девочек для проверки уровня математической подготовки. Какова вероятность, что среди них будут Арина и Олег? (В 11б классе одна Арина; остальные сведения в задаче из 1 варианта).
4. В коробке 6 красных и 8 синих шаров. Ваня достает 3 шара. Какова вероятность, что он вытащит 3 шара одного цвета? Какова вероятность, что он вытащит ровно один синий шар?
5. Денис решает правильно одну задачу из трех, Гриша – одну из двух, а Андрей – одну из шести. Андрей списывает в среднем две задачи из пяти, причем одинаково часто у Гриши и у Дениса. На этот раз задача у Андрея оказалась решенной правильно. Какова вероятность, что он ее списал у Гриши?
6. Имеются 4 карточки с буквами М, А, Ш и А. Маша в произвольном порядке выкладывает их на стол. Какова вероятность, что получится слово МАША?
Вариант 4
1. Р(А)=0,6; Р(В)=0,4; Р(А½В)=0,5. Найти Р(А+В), 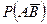 .
.
2. Вероятностное пространство состоит из 4 элементарных исходов: 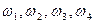 .
. 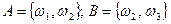 . Известно, что Р(w1)=
. Известно, что Р(w1)= 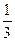 , Р(w3)=
, Р(w3)= 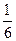 , А и В независимы. Найти вероятности всех элементарных исходов.
, А и В независимы. Найти вероятности всех элементарных исходов.
3. В 11б классе случайным образом выбирают двух мальчиков и двух девочек для проверки уровня физической подготовки. Какова вероятность, что среди них будут две Насти и ни одного Димы? (В 11б классе 3 Димы).
4. В коробке 4 красных и 6 синих шаров. Ваня достает 4 шара. Какова вероятность, что среди них синих шаров окажется больше? Какова вероятность, что синих шаров не будет совсем?
5. У Саши Годикова в левом кармане 4 шпаргалки по физике и 6 по химии, а в правом 2 шпаргалки по химии и шесть по физике. Саша достает из левого кармана одну шпаргалку и, если она по физике, то кладет ее на место, а если по химии, то перекладывает в другой карман. После чего он достает шпаргалку из правого кармана. Известно, что это была шпаргалка по химии. Какова вероятность, что из левого кармана он тоже достал шпаргалку по химии?
6. Имеются 4 карточки с буквами А, Н, Т, О и Н. Антон в произвольном порядке выкладывает их на стол. Какова вероятность, что получится слово ТОННА?
| <== предыдущая страница | | | следующая страница ==> |
| Алгебра событий. Суммой событий А и В называется событие А+В, которое заключается в том, что происходит хотя бы одно из этих событий | | | Географический аспект геополитики |
Дата добавления: 2014-11-15; просмотров: 420; Нарушение авторских прав

Мы поможем в написании ваших работ!