Поле внутри и снаружи проводника

Электростатика проводников

Лекция 3

Мы начнем с изучения постоянных электрических полей, создаваемых заряженными проводниками.

В электростатическом случае:

а) Поле E внутри проводника E = 0

I вариант от противного. Если E≠ 0, то следует возникновение тока, распространение тока связано с диссипацией энергии и потому не может само по себе, без внешнего источника энергии, поддерживаться в стационарном состоянии.

II вариант. Поместим проводник, например металлический, во внешнее электрическое поле или сообщим ему какой-либо заряд. Тогда на все заряды проводника начнет действовать электрическое поле. Отрицательные заряды (электроны в металле квазисвободные и могут относительно свободно перемещаться внутри проводника от атома к атому) сместятся против поля (за малую долю секунды) так, что установится такое распределение зарядов, при котором во всех точках внутри проводника электрическое поле станет нулевым E = 0. То есть, в случае наличия внешнего статическом электрического поля (поля создаваемое сторонними зарядами) в проводнике, изначально даже незаряженного, появляются индуцированные заряды, которые создают во всем пространстве (как внутри, так и снаружи проводника) свое электрическое поле. Поле, создаваемое этими зарядами внутри проводника, полностью компенсирует поле сторонних зарядов.

б) Так как внутри проводника поле E = 0, то плотность избыточных (индуцированных или нескомпенсированных) зарядов внутри проводника также всюду равна нулю (ρ_{инд. внутр.}= 0). Это следует из теоремы Гаусса для вектора E

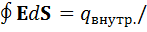ε_ο – Теорема Гаусса для вектора E, (1)

S

т. к. внутри проводника E = 0, то, поток вектора Eсквозь любую замкнутую поверхность внутри проводника также равен нулю. Это значит, что внутри проводника избыточных зарядов нет!

в) Электрические избыточные заряды появляются в проводнике лишь на поверхности проводника с некоторой плотностью σ, в общем случае различной в разных точках поверхности. Избыточный заряд находится в очень тонком поверхностном слое. Его толщина около двух межатомных расстояний: порядка 20А^ο (А^ο – Ангстрем 1А^ο = 10^-8м) в твердом теле и в жидкости; ≈ 100А^ο в газе.

г) Равенство поля E = 0 внутри проводника, согласно связи E с φ

E= – grad φ означает, что φ = const во всех точках внутри проводника, т. е. любой проводник в электрическом стационарном поле представляет собой эквипотенциальную область (φ = const), следовательно, и его поверхность также является эквипотенциальной.

д) Из того, что на поверхности проводника φ = const следует, что у самой этой поверхности поле E перпендикулярноэтой поверхности, т. е.направлено по нормали к ней в каждой точке. Если бы это было не так, то под действием касательной составляющей E_tзаряды пришли бы в движение, и равновесие зарядов было бы невозможным. Итак, E_t= 0 –тангенциальная составляющая электрического поля E_t = 0 на поверхности проводника равна нулю E_t= 0 – это граничное условие для Eна поверхности проводника.

е) Заметим, в точках, не слишком близких к поверхности проводника (тела) среднее поле Eв пустоте фактически совпадает с истинным (микрополем) полем e (и справедливо – д). Эти две величиныEи e отличаются друг от друга лишь на расстояниях в непосредственной близости к телу (на расстояниях менее 20А^ο), где еще сказывается влияние нерегулярных молекулярных полей. Последнее обстоятельство, однако, не отражается на виде усредненных уравнений поля.

ж) Точные микроскопические уравнения Максвелла для стационарного поля в пустоте:

div e = 0 rot e = – ,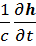

где h – микроскопическая напряженность магнитного поля. Так как среднее магнитное поле предполагается = 0, то и производная < 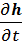> = 0 в результате усреднения равна нулю, и мы находим, что постоянное электрическое поле в пустоте удовлетворяет обычным макроскопическим уравнениям:

div E = 0 rot E = 0,

т. е. является потенциальным: E = – grad φ и потенциал φ удовлетворяет уравнению Лапласа. Δφ = 0 (Δ = 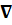²)

При наличии в вакууме свободных зарядов с плотностью ρ_св(r) мы имеем:

div e = 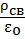; Δφ = – 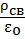– уравнение Пуассона.

Дата добавления: 2014-02-28; просмотров: 638; Нарушение авторских прав

Мы поможем в написании ваших работ!