Поле у поверхности проводника

Пусть на поверхности проводника имеется поверхностный заряд с плотностью σ, тогда напряженность электрического поля E непосредственно у поверхности проводника связана с локальной плотностью поверхностного заряда σ.

Для определения этой связи используем теорему Гаусса. Пусть проводник граничит с вакуумом. Выберем в виде цилиндра замкнутую поверхность S, охватывающую элемент поверхности проводника (внутри и снаружи) площадью dS (см. рис.1). Так как вектор E перпендикулярен

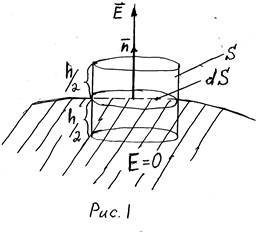
поверхности проводника, то E_┴ dS, поэтому боковую поверхность цилиндра ориентируем перпендикулярно элементу поверхности dS , а торцы параллельно dS. При таком выборе форы замкнутой поверхности поток вектора Eчерез замкнутую поверхность S будет равен только потоку через ее наружный торец (потоки через торец внутри проводника (там E= 0) и боковые поверхности (там Eпараллельно ей) равны нулю). Тогда мы имеем:

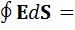E_ndS = q_внутр. / ε_ο = σdS /ε_ο

S

Здесь E_n – проекция вектора Eна внешнюю нормаль n, но |E| = E_n, т. к. E_t = 0. После сокращения dS получаем связь σ с Eна поверхности проводника, граничащего с вакуумом

СИ СГСЕ

|E| = E_n = σ/ε_ο = 4πσ

Это соотношение следует из общего микроскопического уравнения:

div e = 4πρ (ρ – плотность распределения зарядов). После усреднения ρ получаем: div Е = 4π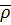, где 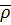– средняя плотность заряда.

Итак, если σ > 0, то E_n > 0, т. е. E_n↑↑n, где n – внешняя нормаль; если σ < 0, то наоборот.

Отметим, что в общем случае полеE вблизи проводника зависит не только от локальной плотности σ заряда на поверхности проводника. Оно определяется всеми зарядами рассматриваемой системы, как и само значение σ.

3. Силы, действующие на поверхность проводника –пондермоторные силы

Пусть заряженный проводник (заряженная поверхность) граничит с вакуумом. Тогда на его элемент поверхности ΔS действует сила ΔFравная

ΔF =σΔSE₀ ,

где σ – поверхностная плотность заряда, σΔS – заряд элемента поверхности ΔS, E₀– напряженность поля, создаваемая в точке нахождения элемента ΔS всеми остальными зарядами системы – заряды, находящиеся вне элемента ΔS. Сразу отметим, что E₀ ≠ Eвблизи данного элемента поверхности ΔS.

Найдем связь поля Eс полемE₀ и соответственно само поле E₀.

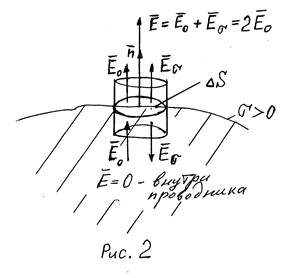
Пусть E_σ – напряженность поля, создаваемая зарядами на площадке вблизи ее поверхности. Размер площадки ΔS выбираем малым настолько, что его можно считать плоским и в его пределах значения σ и, соответственно E₀ и E постоянны. В этом случае элемент ΔS можно считать равномерно заряженной плоскостью. Тогда поле E_σ, создаваемое заряженной плоскостью, можно определить, используя теорему Гаусса (для нашего случая см. рис.2, выбор положения и формы замкнутой поверхности и порядок рассуждений аналогичен действиям, сделанным чуть выше):

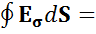2E_σΔS = σΔS /ε_ο,

S

здесьполе E_σ существует как снаружи, так и внутри проводника, причем там и там они равны по величине, но противоположно направлены, при σ >0 они направлены от элемента поверхности ΔS и перпендикулярны ей (как показано на рис.2), поэтому поток вектора E_σ через замкнутую поверхность S равен потоку через два торца цилиндра ΔS и равен 2E_σΔS. Таким образом

E_σ =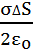
– это величина полей от заряженной плоскости по обе ее стороны, а их направление определяется знаком поверхностного заряда σ и перпендикулярно поверхности.

Внутри проводника поле E равно нулю, и в тоже время равно сумме полей E_σ и E₀, следовательно, по модулю эти поля равны E_σ = E₀ и противоположно направлены. Снаружи проводника эти поля, так же, равны по величине, но направлены в одну сторону и тогда , т.к. поле E равно (его значение мы определили в предыдущем пункте 2.)

E = 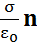= E_σ + E₀ = 2 E₀ ,

здесь n наружная нормаль к поверхности проводника в точке определения поля. Отсюда

E₀ = .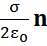

И тогда сила ΔF, действующая на элемент поверхности ΔS равна

ΔF = σΔSE₀ =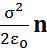ΔS ,

а сила F, действующая на единицу поверхности, или поверхностная плотность сил (F =ΔF/ΔS) будет имеет вид:

F =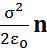

Видно, что независимо от знака σ и направления вектора поля E вблизи поверхности, силаF всегда направлена наружу от проводника (как и наружная нормаль n), стремясь его растянуть.

Дата добавления: 2014-02-28; просмотров: 485; Нарушение авторских прав

Мы поможем в написании ваших работ!