
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Перевод чисел из одной системы счисления в другую
Наиболее часто встречающиеся системы счисления - это двоичная, шестнадцатеричная и десятичная. Как же связаны между собой представления числа в различных системах счисления? Рассмотрим различные способы перевода чисел из одной системы счисления в другую на конкретных примерах.
Пусть требуется перевести число 567 из десятичной в двоичную систему. Сначала определим максимальную степень двойки, такую, чтобы два в этой степени было меньше или равно исходному числу. В нашем случае это 9, т. к. 29=512, а 210=1024, что больше начального числа. Таким образом, мы получим число разрядов результата. Оно равно 9+1=10. Поэтому результат будет иметь вид 1ххххххххх, где вместо х могут стоять любые двоичные цифры. Найдем вторую цифру результата. Возведем двойку в степень 9 и вычтем из исходного числа: 567-29=55. Остаток сравним с числом 28=256. Так как 55 меньше 256, то девятый разряд будет нулем, т. е. результат примет вид 10хххххххх. Рассмотрим восьмой разряд. Так как 27=128>55, то и он будет нулевым.
Седьмой разряд также оказывается нулевым. Искомая двоичная запись числа принимает вид 1000хххххх. 25=32<55, поэтому шестой разряд равен 1 (результат 10001ххххх). Для остатка 55-32=23 справедливо неравенство 24=16<23, что означает равенство единице пятого разряда. Действуя аналогично, получаем в результате число 1000110111. Мы разложили данное число по степеням двойки:
567=1*29+0*28+0*27+0*26+1*25+1*24+0*23+1*22 +1*21+1*20
При другом способe перевода чисел используется операция деления в столбик. Рассмотрим то же самое число 567. Разделив его на 2, получим частное 283 и остаток 1. Проведем ту же самую операцию с числом 283. Получим частное 141, остаток 1. Опять делим полученное частное на 2, и так до тех пор, пока частное не станет меньше делителя. Теперь для того, чтобы получить число в двоичной системе счисления, достаточно записать последнее частное, то есть 1, и приписать к нему в обратном порядке все полученные в процессе деления остатки.
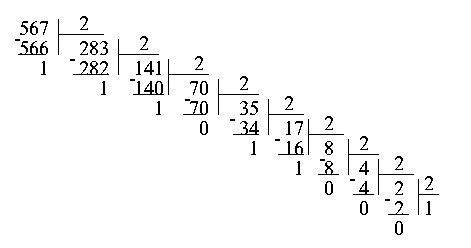
Результат, естественно, не изменился: 567 в двоичной системе счисления записывается как 1000110111.
Эти два способа применимы при переводе числа из десятичной системы в систему с любым основанием. Для закрепления навыков рассмотрим перевод числа 567 в систему счисления с основанием 16.
Сначала осуществим разложение данного числа по степеням основания. Искомое число будет состоять из трех цифр, т. к. 162=256 < 567 < 163=4096. Определим цифру старшего разряда. 2*162=512<567<3*162=768, следовательно искомое число имеет вид 2хх, где вместо х могут стоять любые шестнадцатеричные цифры. Остается распределить по следующим разрядам число 55 (567-512). 3*16=48<55<4*16=64, значит во втором разряде находится цифра 3. Последняя цифра равна 7 (55-48). Искомое шестнадцатеричное число равно 237.
Второй способ состоит в осуществлении последовательного деления в столбик, с единственным отличием в том, что делить надо не на 2, а на 16, и процесс деления заканчивается, когда частное становится строго меньше 16.
Конечно, не надо забывать и о том, что для записи числа в шестнадцатеричной системе счисления, необходимо заменить 10 на A, 11 на B и так далее.

Операция перевода в десятичную систему выглядит гораздо проще, так как любое десятичное число можно представить в виде x = a0*pn + a1*pn-1 + ... + an-1*p1 + an*p0, где a0 ... an - это цифры данного числа в системе счисления с основанием p.
Пример. Переведем число 4A3F в десятичную систему. По определению, 4A3F= 4*163+A*162+3*16+F. Заменив A на 10, а F на 15, получим 4*163+10*162+3*16+15= 19007.
Пожалуй, проще всего осуществляется перевод чисел из двоичной системы в системы с основанием, равным степеням двойки (8 и 16), и наоборот. Для того чтобы целое двоичное число записать в системе счисления с основанием 2n, нужно
- данное двоичное число разбить справа налево на группы по n-цифр в каждой;
- если в последней левой группе окажется меньше n разрядов, то дополнить ее нулями до нужного числа разрядов;
- рассмотреть каждую группу, как n-разрядное двоичное число, и заменить ее соответствующей цифрой в системе счисления с основанием 2n.
| Двоично-шестнадцатеричная таблица | |||||||||||||||||
| 2-ная | |||||||||||||||||
| 16-ная | |||||||||||||||||
| 2-ная | |||||||||||||||||
| 16-ная | A | B | C | D | E | F | |||||||||||
| Двоично-восьмеричная таблица | |||||||||||||||||
| 2-ная | |||||||||||||||||
| 8-ная | |||||||||||||||||
| <== предыдущая страница | | | следующая страница ==> |
| Ная и 16-ная системы счисления | | | Сущность налогов и их функции |
Дата добавления: 2014-02-28; просмотров: 1680; Нарушение авторских прав

Мы поможем в написании ваших работ!