
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
УСЛОВНЫЕ (ИМПЛИКАТИВНЫЕ) ВЫСКАЗЫВАНИЯ
В) Простая дизъюнкция
Простая дизъюнкция (разделение) — логический союз, соответствующий двум смысловым значениям грамматического союза «или», «либо». С помощью этого союза образуются разделительные, или дизъюнктивные высказывания.
Разделительными называются сложные высказывания, состоящие из двух и более простых, соединенных логическим союзом «или». Простые высказывания в составе сложного называются членами дизъюнкции, или дизъюнктами, а название союза переносится на сложное высказывание.
Дизъюнкция бывает полной, или закрытой, если в ней перечислены
все возможные случаи, и неполной, или открытой, когда перечислены только некоторые из возможных случаев. Так, высказывание «Деревья бывают или лиственные, или хвойные» представляет собой закрытую дизъюнкцию, ибо предполагается, что других деревьев, кроме лиственных и хвойных, не существует, а высказывание «Леса бывают или лиственные, или хвойные» — открытую так как, кроме перечисленных, существуют еще смешанные леса.
В естественном языке союз «или» может употребляться в двух смыслах:
соединительно-разделительном, когда он связывает характеристики не исключающие друг друга и совмещаемые в одном предмете, или такие причины, которые вызывают одно и то же следствие, действуя в отдельности или вместе, истрого-разделительном, если выраженные членами дизъюнкции характеристики не могут совмещаться в одном предмете. В высказывании «Эффективность производства достигается или повышением производительности труда, или укоренением новых технологий, или повышением цены на производимый продукт» союз «или» употреблен в соединительно-разделительном смысле и может быть заменен союзом «и». В высказывании «По объему имя может быть или единичным, или общим, или нулевым» тот же союз связывает не совместимые в одном предмете признаки. Первый смысл союза «или» называется слабой дизъюнкцией, а второй — строгой дизъюнкцией.
Слабой дизъюнкцией, таким образом, является такое высказывание, в котором утверждается истинность по крайней мере одного из простых высказываний. Когда, например, узнав, что кто-то хорошо разбирается в автомобилях, мы выскажем предположение, что он или механик, или водитель, мы не ошибемся, если этот человек окажется:
а) механиком и водителем; б) механиком, но не водителем; в) водителем, но не механиком. Наше предположение будет ложным только в том случае, когда человек, о котором мы высказали предположение, не имеет никакого отношения к названным профессиям.
| P | Q | ( P V Q ) |
| и | и | и |
| и | л | и |
| л | и | и |
| л | л | л |
Зависимость логического значения разделительного высказывания со слабой дизъюнкцией от логического значения ее членов показано в выше приведенной таблице. Слабая дизъюнкция истинна только тогда, когда по крайней мере один ее член истинен, и ложна, когда все ее члены ложны.
Строгая дизъюнкция — это сложное высказывание, в котором утверждается, что из образующих его простых высказываний только одно истинное, а остальные ложны. Она отличается от слабой дизъюнкции тем, что в последней допустима истинность всех членов дизъюнкции, а в строгой - истинность одного из ее членов исключает истинность остальных. Строгую дизъюнкцию высказывают в тех случаях, если знают, что из двух или более предположений только одно истинное, хотя и не знают, какое именно.
Зависимость логического значения строгой дизъюнкции от логических значений ее членов показана в ниже приводимой таблице.
Строгая дизъюнкция (иногда ее называют исключающей) истинна только тогда, когда лишь один ее член истинен, а остальные — ложны.
| P | Q |  ( P V Q ) ( P V Q )
|
| и | и | л |
| и | л | и |
| л | и | и |
| л | л | л |
Условными называются сложные высказывания, состоящие из двух частей, связанных между собой логическим союзом «если, то». Часть со словом «если» называется основанием, или антецедентом, а часть словом «то» — следствием, или консеквентом. В высказывании «Если человек болен, то он не может трудиться» первая часть «если человек болен» — основание, а вторая — «то он не может трудиться» — следствие.
В естественном языке союз «если, то» употребляется по меньшей мере в четырех смыслах и, соответственно, выражает столько же различных логических союзов. Союз «если, то», во-первых, употребляется в смысле «если р, то обязательно q». «Если спираль перегорит, то электрический чайник выйдет из строя». ( Прямая импликация, или просто импликация)
Во-вторых, он может употребляться в смысле «если р, то, возможно, q», или « только если p, то q» — «Если мы будем в Париже, то посетим Лувр» (обратная импликация, или репликация). В-третьих, союз «если, то» употребляется в смысле «если и только если р, то
q», или «p тогда и только тогда, когда q» — «Если треугольник равносторонний, то он — равноугольный» (двойная импликация, или эквиваленция). В-четвертых, союз «если, то» может употребляться в смысле соединительного союза «а». «Если вчера стояла хорошая погода, то сегодня идет дождь».
На приведенных выше примерах рассмотрим, как зависит
логическое значение сложного высказывания от логического
значения его составных частей.
Первый пример может описывать следующие ситуации:
а) спираль перегорела, и электрический чайник вышел из строя;
б) спираль перегорела, но электрический чайник не вышел из строя;
в) спираль не перегорела, но электрический чайник вышел из строя;
г) спираль не перегорела, и электрический чайник не вышел из строя.
Нетрудно заметить, что невозможной является только вторая
ситуация.
Таким образом, импликация ложна только тогда, когда основание истинно, а следствие ложно. Из ситуаций, которые могут быть описаны вторым примером, невозможной является третья, т.е. невозможно посетить Лувр, не побывав в Париже. Таким образом, репликация ложна только тогда, когда основание ложно, а следствие истинно.
Из содержания третьего примера следует, что невозможно, чтобы треугольник был равносторонним, но не был равноугольным, или был равноугольным, но не был равносторонним. Поэтому эквиваленция истинна только тогда, когда обе ее части либо истинны, либо ложны. Приведем сводную таблицу связи суждений с помощью этих логических союзов.
| P | Q | P → Q (импликация) | 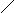 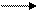 P Q
( реимпликация) P Q
( реимпликация)
| P ↔ Q (эквиваленция) |
| И | И | И | И | И |
| И | Л | Л | И | Л |
| Л | И | И | Л | Л |
| Л | Л | И | И | И |
| <== предыдущая страница | | | следующая страница ==> |
| Сложные суждения | | | ОТНОШЕНИЯ МЕЖДУ СЛОЖНЫМИ ВЫСКАЗЫВАНИЯМИ |
Дата добавления: 2014-02-26; просмотров: 759; Нарушение авторских прав

Мы поможем в написании ваших работ!