Манипулирование данными

Как уже говорилось ранее для управления отношениями в реляционных СУБД можно использовать процедурные и непроцедурные языки. Коддом были предложены формальные (а не дружественные пользователю) языки – реляционная алгебра и реляционное исчисление.

Реляционная алгебра представляет процедурный язык, который может быть использован, чтобы сообщить СУБД как следует построить требуемое отношение на базе одного или нескольких существующих в базе данных отношений.

Реляционное исчисление представляет собой непроцедурный язык, который можно использовать для определения того, каким будет некоторое отношение, созданное на основе одного или нескольких других отношений базы данных.

Реляционная алгебра и реляционное исчисление эквивалентны друг другу. Для каждого выражения алгебры существует эквивалентное выражение в реляционном исчислении (и наоборот).

Необходимо различать сами отношения (то есть значения отношений) и переменные-отношения, так как отношения являются переменными (в математическом смысле), над которыми можно осуществлять определенные действия – конструировать новые отношения, изменять их значения и т.д.

Кодд определил восемь операторов реляционной алгебры, использующих отношения в качестве операндов и возвращающих отношения в качестве результата.

Восемь операторов составляют две группы по четыре оператора:

1. Традиционные операции над множествами – объединение, пересечение, разность и декартово произведение (с учетом того, что их операндами являются отношения, а не произвольные множества).

2. Специальные реляционные операции – выборка, проекция, соединение и деление.

5.5.1. Специальные реляционные операции

Выборка

Рис.14 Реляционная операция – выборка

Результат операции выборка - отношение, содержащее все кортежи из заданного отношения, удовлетворяющие определенным условиям (рис 14).

Проекция

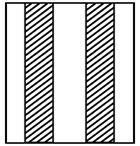
Рис.15 Реляционная операция - проекция

Результат операции проекция - отношение, содержащее кортежи заданного отношения, состоящие из определенных атрибутов (остальные атрибуты исключены) (рис.15).

Соединение

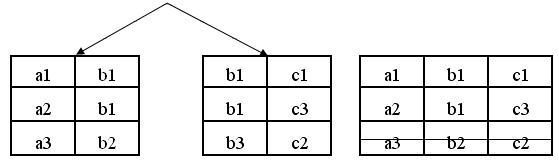
Рис.16 Реляционная операция - соединение

Результат операции соединение - отношение, содержащее все возможные кортежи, которые представляют собой комбинацию атрибутов двух кортежей, принадлежащих двум заданным отношениям, при условии, что в этих двух комбинируемых кортежах присутствуют одинаковые значения в одном или нескольких общих для исходных отношений атрибутах (причем эти общие значения в результирующем кортеже появляются один раз, а не дважды) (рис.16).

Деление

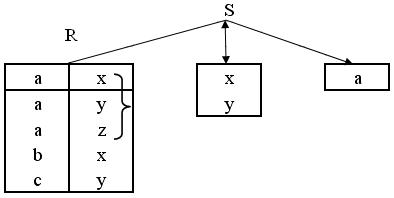
Рис.17 Реляционная операция - деление

Результат операции деления для заданных двух отношений (унарных) и одного бинарного - отношение, содержащее все кортежи из первого унарного отношения, которые содержатся также в бинарном отношении и соответствуют всем кортежам во втором унарном отношении (рис.17).

Результатом оператора деления R на S является набор кортежей отношения R, определенных на множестве атрибутов не входящих в S, которые соответствуют комбинации всех кортежей отношения S.

5.5.2. Традиционные операции над множествами

Объединение

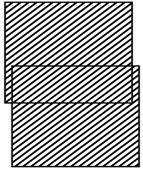
Рис. 18 Операция объединение

Результат операции объединение - отношение, содержащее все кортежи, которые принадлежат либо одному из двух заданных отношений, либо им обоим (рис. 18).

Произведение

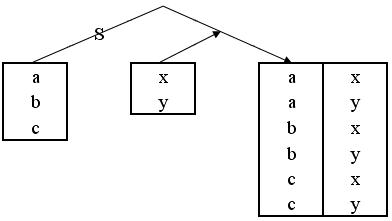
Рис. 19 Операция произведение

Результат операции произведение - отношение, содержащее все возможные кортежи, которые являются сочетанием двух кортежей, принадлежащих соответственно двум заданным отношениям.

Пересечение

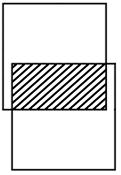
Рис. 20. Операция пересечение

Результат операции пересечение - отношение, содержащее все кортежи, которые принадлежат одновременно двум заданным отношениям. (рис. 20).

Разность

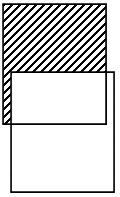
Рис. 21. Операция разность

Результат операции разность - отношение, содержащее все кортежи, которые принадлежат первому из двух заданных отношений и не принадлежат второму (рис.21).

Так как результатом выполнения любой операции является отношение, то можно записывать вложенные реляционные выражения, то есть выражения, в которых операнды сами представлены реляционными выражениями, причем произвольной сложности.

Основная цель алгебры – обеспечить запись реляционных выражений. Выражения можно преобразовывать в соответствии с правилами преобразования. Таким образом, реляционная алгебра может служить хорошим обоснованием для построения оптимизатора запросов СУБД.

Реляционная алгебра в явном виде представляет набор операций, которые можно использовать, чтобы сообщить системе, как в базе данных из определенных отношений построить некоторое требуемое отношение. Реляционное исчисление просто представляет систему обозначений для определения требуемого отношения в терминах данных отношений.

Дата добавления: 2014-02-28; просмотров: 365; Нарушение авторских прав

Мы поможем в написании ваших работ!