Экстремумы функции

Определение 4.Точка x₀ называется точкой минимума (максимума) функции y=f(x), если она определена в некоторой окрестности этой точки и для каждой точки x ≠x₀ этой окрестности f(x) > f(x₀) (соответственно f(x) < f(x₀)). Значение функции f(x₀) называется минимумом (соответственно максимумом).

На рисунке 2а b – точка минимума, c – точка максимума.

Под экстремумом понимается либо минимум, либо максимум.

Точка x₀ из области определения функции y=f(x), называется критической точкой, если либо f(x) дифференцируема в x₀ и f ¢(x₀) = 0, либо f(x) не дифференцируема в x₀. На рис. 2б и 2в точка x₀ – критическая.

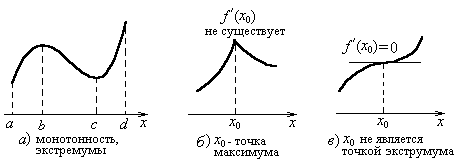Рисунок 2

Необходимое условие экстремума. Если x₀ - точка экстремума функции f (x), то она является критической точкой этой функции.

На рис. 2б критическая точка x₀ является точкой экстремума, а на рис. 2в критическая точка x₀ не является точкой экстремума. Таким образом, не всякая критическая точка является точкой экстремума.

Первое достаточное условие экстремума.Пусть x₀ - критическая точка функции y=f(x). Если в некоторой окрестности точки x₀ слева от нее производная f ¢(x) принимает один знак, а справа от нее - противоположный, то x₀- точка экстремума. При этом если слева f’(x)>0, справа f ¢(x)<0, то x₀- точка максимума, в противном случае x₀- точка минимума. Если в некоторой проколотой окрестности точки x₀ производная f ¢(x) принимает один знак, то x₀ не является точкой экстремума. Если к тому же f (x) непрерывна в x₀, то функция монотонна в этой окрестности (рис. 2в).

Второе достаточное условие экстремума. Пусть f ¢(x₀)=0 и существует f′′( x₀). Тогда если f ′′( x₀)>0, то x₀- точка максимума. Если же f ′′( x₀)<0, то x₀- точка минимума.

Этим достаточным условием экстремума удобно пользоваться, если достаточно сложно установить знак первой производной в окрестности точки экстремума.

Дата добавления: 2014-02-28; просмотров: 608; Нарушение авторских прав

Мы поможем в написании ваших работ!