Правило нахождения точек экстремума и промежутков монотонности

1) Найти область определения функции f(x).

2) Найти все критические точки функции f(x). Для этого найти производную, решить уравнение f ¢(x)=0 и найти точки x из области определения, в которых f ¢(x) не существует.

3) Разбить область определения критическими точками на промежутки и в них найти знаки производной.

4) В промежутках, где производная положительна, функция возрастает, а в промежутках, где производная отрицательна, функция убывает.

5) Точки экстремума ищем среди критических точек. Пусть x₀ – критическая точка. Если в интервале слева от x₀ производная положительна (отрицательна), а справа отрицательна (положительна), то x₀ - точка максимума (минимума).

Замечание 10. Если в интервале слева и справа от x₀ производная имеет один и тот же знак, то x₀ не является точкой экстремума. При этом, если функция непрерывна в этой точке, то функция монотонна в целом в этих двух интервалах (рис 3а).

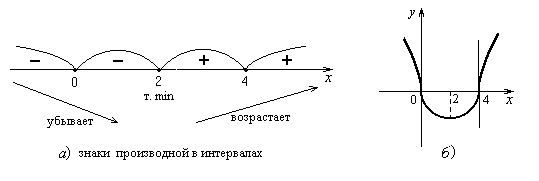Рисунок 3

Пример.13) Исследовать функцию 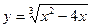на экстремум и монотонность.

Решение. 1) Область определения – множество всех действительных чисел R.

2)

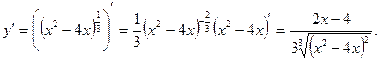
Найдем критические точки. Решим уравнение y¢ = 0: 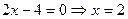-критическая. y¢ не существует при 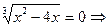x (x – 4) = 0 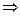x = 0 или 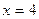. Эти точки входят в область определения функции, следовательно, являются критическими.

3) Разобьем область определения R критическими точками 0, 2, 4 на интервалы (– ∞, 0), (0, 2), (2, 4), (4, +∞) (рис. 3а), в каждой из которых производная сохраняет знак. Найдем знаки производной в этих интервалах. Для этого выберем по одной точке из этих интервалов (например, –1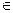(– ∞, 0), 1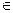(0, 2), 3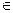(2, 4), 5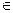(4, +∞)) и определим знаки производной y¢ в этих точках: y¢(-1) < 0, y¢(1) < 0, y¢(3) > 0, y¢(5) > 0. Следовательно, y¢ < 0 в интервалах (– ∞, 0), (0, 2) и y¢ > 0 в интервалах (2, 4), (4, +∞).

4) Функция убывает в интервалах (– ∞, 0) и (0, 2), возрастает в интервалах (2, 4) и (4, +∞). Однако можно сделать более сильный вывод. В самом деле, в окрестностях критических точек x = 0 и x = 4 производная не меняет знака, значит, они не являются точками экстремума. В силу замечания 10 функция убывает в интервале (– ∞, 2) и возрастает в интервале (2, +∞). Заметим, что y¢(0) = – ∞, y¢(4) = +∞, следовательно, в точках (0, 0) и (4, 0) касательные параллельны оси Оу (рис.3б).

5) Критическая точка x = 2 является точкой минимума (рис. 3а).

На рисунке 3б изображен схематически график функции .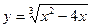

12. Направление выпуклости функции. Точки перегиба.Пусть функция y=f(x) имеет конечную или бесконечную производную в каждой точке интервала Х = (а, b). Обозначим Г(Х) дугу графика функции f(x), соответствующую интервалу X.

Определение 5.Если дуга Г(Х) лежит не ниже (не выше) касательной к графику функции y=f(x), проведенной в любой точке M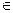Г(Х), то функция или график функции называется выпуклым вниз (соответственно выпуклым вверх) в интервале X (рис. 4а).

Точка на графике функции, в которой существует касательная к графику функции, называется точкой перегиба функции или графика функции, если она является границей дуг графика с разными направлениями выпуклости (рис. 4б,4в).

Рисунок 4

Заметим, что в точке перегиба требуется существование касательной к графику.

В некоторых учебных пособиях выпуклую вверх функцию называют выпуклой, а выпуклую вниз функцию - вогнутой. Мы будем также пользоваться этими терминами, когда это удобно.

Теорема 4 (достаточное условие выпуклости вверх и вниз). Если функция f(x) дифференцируема дважды в интервале 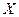и в ней f ² (x) > 0 (f ²(x) < 0), то f(x) является выпуклой вниз (соответственно выпуклой вверх) в интервале X.

Необходимое условие точки перегиба. Если M₀ (x₀, f(x₀)) - точка перегиба функции f(x), то либо и f ²(x₀) = 0, либо f ²(x₀) не существует (рис. 4б, 4в). Следовательно, абсциссы точек перегиба нужно искать в тех значениях x, при которых вторая производная либо равна нулю, либо не существует.

Достаточное условие точки перегиба.Пусть функция f(x) имеет производную (может быть бесконечную) в точке x₀, существует вторая производная в проколотой окрестности точки x₀ и либо f ²(x₀) = 0, либо f ²(x₀) не существует. Тогда если при переходе через x₀ f ²(x) меняет знак, то (x₀, f(x₀)) является точкой перегиба.

Дата добавления: 2014-02-28; просмотров: 973; Нарушение авторских прав

Мы поможем в написании ваших работ!