Правило нахождения точек перегиба и промежутков выпуклости вверх и вниз

1) Найти область определения функции f(x).

2) Найти f ²(x) и решить уравнение f ²(x) = 0 и найти точки x из области определения, в которых f ²(x) не существует.

3) Разбить область определения найденными в предыдущем пункте точками на промежутки и в них найти знаки второй производной.

4) Согласно теореме 4 в промежутках, где вторая производная положительна, функция выпукла вниз, а в промежутках, где вторая производная отрицательна, функция выпукла вверх.

5) В соответствии с необходимым условием абсциссы точек перегиба нужно искать среди значений, найденных в пункте 2. Пусть x₀ - такое значение. Если производная в точке x₀ (конечная или бесконечная) существует и в интервалах непосредственно слева и справа от x₀ вторая производная имеет разные знаки, то x₀ - абсцисса точки перегиба.

Пример.14) Исследовать функцию на выпуклость, вогнутость, найти точки перегиба.

Решение. 1) Функция определена при всех действительных значениях x, таких, что x^­­2-4 ¹­­ 0, т.е. x ¹ ±2.

2) Найдем вторую производную.

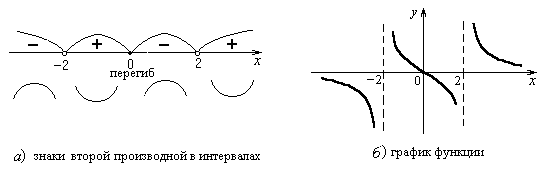Рисунок 5

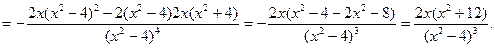
y²=0 при x = 0. y² не существует при x = ±2, но они не входят в область определения функции, поэтому они не могут быть абсциссами точек перегиба.

3) Разобьем область определения точкой x = 0 на интервалы (– ∞, -2), (-2, 0), (0, 2), (2, +∞), в каждом из которых вторая производная сохраняет знак.

Определим знак второй производной в каждом из этих интервалов. В точке x=-3 из интервала (– ∞, -2) y²< 0, следовательно, y²< 0 во всем интервале (– ∞, -2). Аналогично определяем, что y² > 0 в интервалах (-2, 0) и (2, +∞), y² < 0 в интервале (0, 2) (рис. 5а).

4) Функция выпукла вверх в интервалах (– ∞, -2), (0, 2), выпукла вниз в интервалах (-2, 0), (2, +∞).

5) В интервалах (-2, 0), (0, 2) y² имеет разные знаки. Значит, (0, 0) является точкой перегиба функции.

На рисунке 5б приведен схематически график функции.

13. Асимптоты графика функции.Пусть M(x, y) - точка графика функции y=f(x). Будем говорить, что точка M бесконечно удаляется в бесконечность по графику, если она движется по графику так, что либо x → ± ∞,либо y→ ± ∞. При этом считаем, что функция определена в соответствующих множествах.

Определение 6.Прямая называется асимптотой графика функции y = f(x), если при удалении точки M в бесконечность по графику, расстояние от M до этой прямой стремится к нулю (рис. 6а).

Вертикальная (горизонтальная) асимптота - это асимптота, параллельная оси Оу (соответственно Ох). Остальные асимптоты называются наклонными.

На рис. 6б и 6в прямые х = 2, х = 0 и х = -1 являются вертикальными асимптотами, прямая у = 1 - горизонтальной, прямая у = х+2 - наклонной.

Нахождение вертикальных асимптот.Если x₀- точка бесконечного разрыва функции y = f(x), то прямая x = x₀ является вертикальной асимптотой. Например, если

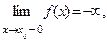
то точка графика при y → -∞ бесконечно близко приближается к вертикальной асимптоте x = x₀ с левой стороны (рис. 6в, x₀= -1).

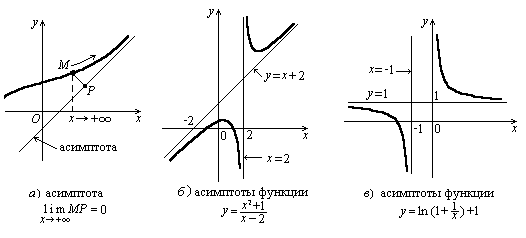Рисунок 6

Вертикальная асимптота может быть в точке, являющейся границей области определения функции, если односторонний предел в этой точке равен +∞ или -∞ (рис. 6в).

Нахождение горизонтальных асимптот.Если

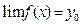при x →+ ∞ (или -∞),

то прямая y = y₀ является горизонтальной асимптотой при x →+ ∞ (или -∞).

Нахождение наклонных асимптот.Уравнение наклонной асимптоты имеет вид

y= kx+b , где угловой коэффициент k ≠ 0. Коэффициенты k и b при x →+∞ (-∞) находят по формулам:

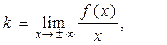
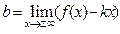. (7)

Замечание 11. В формулах (7) подразумевается, что оба предела существуют и конечны. Если хотя бы один из них не существует, то наклонной асимптоты нет.

Замечание 12.Если пределы (7) конечны и k = 0, то график имеет горизонтальную асимптоту y= b при x →+ ∞ (или -∞). Поэтому если существует горизонтальная асимптота при x →+ ∞ (или -∞), то нет наклонной асимптоты при x →+ ∞ (или -∞).

Примеры. 15) Найти асимптоты графика функции .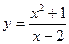

Решение. Точка x = 2 является точкой разрыва функции. Найдем односторонние пределы функции в этой точке

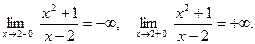
Следовательно, прямая x = 2 является вертикальной асимптотой при у→ + ∞ и у→ -∞.

Дата добавления: 2014-02-28; просмотров: 723; Нарушение авторских прав

Мы поможем в написании ваших работ!