
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
О других методах. Особые случаи
Кроме рассмотренных выше методов численного интегрирования существует ряд других. Дадим краткий обзор некоторых из них.
Формулы Ньютона -Котеса получаются путем замены подынтегральной функции интерполяционным многочленом Лагранжа с разбиением отрезка интегрирования на 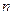 равных частей. Получающиеся формулы используют значения подынтегральной функции в узлах интерполяции и являются точными для всех многочленов некоторой степени, зависящей от числа узлов.(Точность формул растет с увеличением степени интерполяционного многочлена).
равных частей. Получающиеся формулы используют значения подынтегральной функции в узлах интерполяции и являются точными для всех многочленов некоторой степени, зависящей от числа узлов.(Точность формул растет с увеличением степени интерполяционного многочлена).
Метод Гаусса не предполагает разбиения отрезка интегрирования на равные промежутки. Формулы численного интегрирования интерполяционного типа ищутся такими , чтобы они обладали наивысшим порядком точности при заданном числе узлов. Узлы и коэффициенты формул численного интегрирования находятся из условий обращения в нуль их остаточных членов для всех многочленов максимально высокой степени.
Формула Эрмита, являющаяся частным случаем формул Гаусса, использует многочлены Чебышева для вычисления интегралов вида 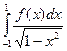 .
.
Получающаяся формула характерна тем, что все коэффициенты при  равны.
равны.
Метод Маркова состоит в том, что при выводе формул Гаусса вводятся дополнительные предположения о совпадении точек разбиения отрезка, по крайней мере, с одним из его концов.
Формула Чебышева представляет интеграл в виде 
При этом решается следующая задача: найти точки 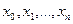 и коэффициент
и коэффициент 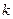 такие, при которых остаточный член
такие, при которых остаточный член  обращается в нуль, когда функция
обращается в нуль, когда функция  является произвольным многочленом возможно большей степени.
является произвольным многочленом возможно большей степени.
Формула Эйлера использует не только значения подынтегральной функции в точках разбиения, но и ее производные до некоторого порядка на границах отрезка.
Рассмотрим особые случаи численного интегрирования: а) подынтегральная функция разрывна на отрезке интегрирования; б) несобственные интегралы.
а) В ряде случаев подынтегральная функция  или ее производные в некоторых внутренних точках
или ее производные в некоторых внутренних точках 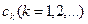 отрезка интегрирования
отрезка интегрирования  терпят разрыв. В этом случае интеграл вычисляют численно каждого участка непрерывности и результаты складывают. Например, в случае одной точки разрыва
терпят разрыв. В этом случае интеграл вычисляют численно каждого участка непрерывности и результаты складывают. Например, в случае одной точки разрыва 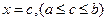 имеем
имеем
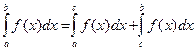 .
.
Для вычисления каждого из стоящих в правой части интегралов можно использовать рассмотренные выше методы.
б) Не так просто обстоит дело с вычислением несобственных интегралов. Напомним, что к такому типу относятся интегралы, которые имеют хотя бы одну бесконечную границу интегрирования или подынтегральную функцию, обращающуюся в бесконечность хотя бы в одной точке отрезка интегрирования.
Рассмотрим сначала интеграл с бесконечной границей интегрирования, например интеграл вида
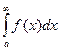 ,
, 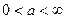 .
.
Существует несколько приемов вычисления таких интегралов.
Можно попытаться ввести замену переменных  , которая превращает интервал интегрирования
, которая превращает интервал интегрирования 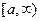 в отрезок
в отрезок 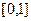 . При этом подынтегральная функция и первые ее производные до некоторого порядка должны оставаться ограниченными.
. При этом подынтегральная функция и первые ее производные до некоторого порядка должны оставаться ограниченными.
Еще один прием состоит в том, что бесконечная граница заменяется некоторым достаточно большим числом 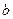 так, чтобы принятое значение интеграла отличалось от исходного на некоторый малый остаток, т. е.
так, чтобы принятое значение интеграла отличалось от исходного на некоторый малый остаток, т. е.
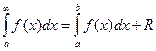 ,
, 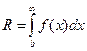 .
.
Если функция обращается в бесконечность в некоторой точке  конечного отрезка интегрирования, то можно попытаться выделить особенность, представив подынтегральную функцию в виде суммы двух функций:
конечного отрезка интегрирования, то можно попытаться выделить особенность, представив подынтегральную функцию в виде суммы двух функций:
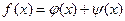 .
.
При этом 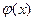 ограничена, а
ограничена, а  имеет особенность в данной точке, но интеграл (несобственный) от нее может быть вычислен непосредственно по формулам. Тогда численный метод используется только для интегрирования ограниченной функции
имеет особенность в данной точке, но интеграл (несобственный) от нее может быть вычислен непосредственно по формулам. Тогда численный метод используется только для интегрирования ограниченной функции 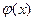 .
.
| <== предыдущая страница | | | следующая страница ==> |
| Использование сплайнов | | | Кратные интегралы |
Дата добавления: 2014-03-01; просмотров: 564; Нарушение авторских прав

Мы поможем в написании ваших работ!