
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Произвольная система сил
Задача 5
Задача 4
Составная балка состоит из двух участков АС и СД, соединенных в точке с шарниром (рис. 13). В точке А – неподвижная опора, в точке В – подвижная опора, конец Д балки поддерживается с помощью вертикальной тяги ДЕ. К балке СД приложена вертикальная сила F. Найти реакцию в шарнире ДЕ. Известно 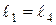 и
и 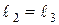 .
.
Решение: Используя принцип освобождаемости от связей, заменим действие связей соответствующими реакциями. Реакцию в шарнире А представим в виде двух составляющих XA и YA . Реакцию подвижной опоры обозначим RB , а реакцию нити – Т. В шарнире С разделим балку на два тела: стержень АС и стержень СД и для каждого участка в точке С обозначим равнодействующую внутренних сил в виде XC , YC и 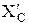 ,
, 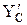 .
.
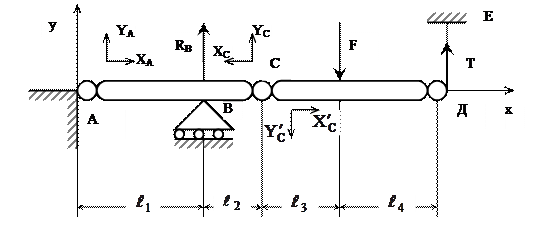

Рис. 13
Составим уравнения равновесия для участка АС
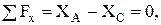 (1)
(1)
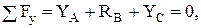 (2)
(2)
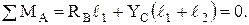 (3)
(3)
Уравнения равновесия для участка СД
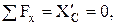 (4)
(4)
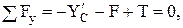 (5)
(5)
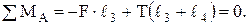 (6)
(6)
Учитывая равенства 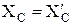 и
и 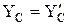 получим:
получим:
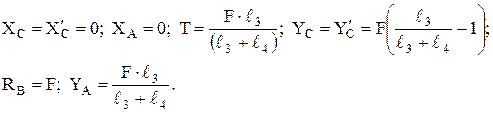
Для данной стержневой конструкции, представленной на рис. 14, определить величины опорных реакций.
Решение: Стержневая конструкция состоит из двух частей АС и ВС. Используя принцип освобождаемости от связей, заменим опоры их реакциями. Для жестко защемленной опоры А имеем три составляющих опорной реакции, для шарнирно подвижной опоры В – одну опорную реакцию. В точке разделения конструкции С имеем по две составляющих (для каждого участка) реакций внутренних связей, который будут попарно равны по модулю и противоположны по направлению.
Составим уравнения равновесия для участка АС.
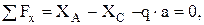 (1)
(1)
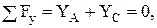 (2)
(2)
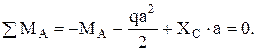 (3)
(3)
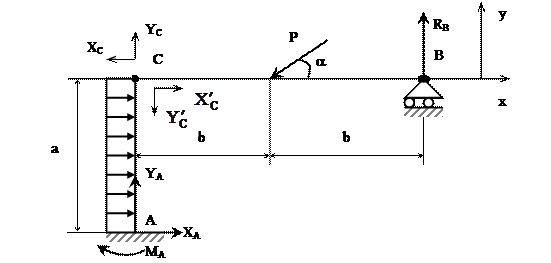

Рис. 14
Составим уравнения равновесия для участка ВС.
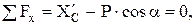 (4)
(4)
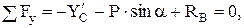 (5)
(5)
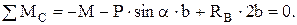 (6)
(6)
Из полученных шести уравнений, учитывая при этом равенства 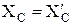 ,
, 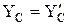 можно найти величины опорных реакций.
можно найти величины опорных реакций.
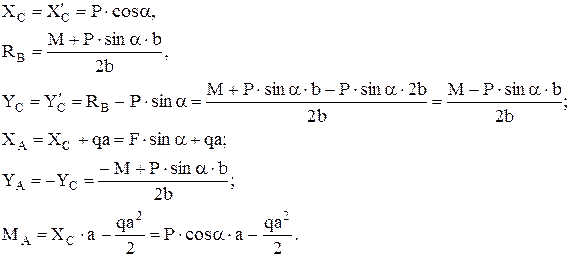
Произвольной будем называть систему сил линии действия, которых расположены как угодно в пространстве. При изучении произвольной системы сил необходимо ознакомиться с понятием момента силы относительно оси.
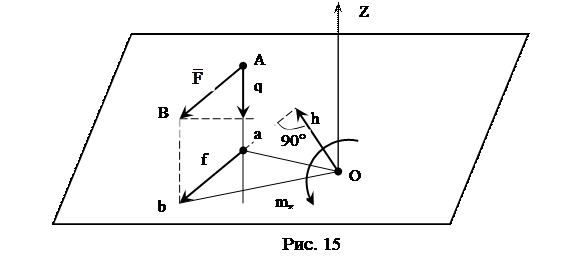
Пусть известна сила F, произвольно расположенная в пространстве. Разложим эту силу на две составляющие: одну параллельную оси Z, и другую f, лежащую на плоскости перпендикулярной оси Z. Опустим перпендикуляр на линию действия силы f и обозначим его h (рис. 15). Мерой вращательного эффекта, создаваемого силой f, будет служить момент силы относительно точки пересечения оси Z с плоскостью. Следовательно, величиной момента силы будет являться взятое с соответствующим знаком произведение mz = ±f∙h.
Из определения момента и из рис. 15 можно сделать следующие выводы:
1. Момент силы относительно оси равен нулю в том случае, когда линия действия силы пересекает ось или когда сила параллельна этой оси.
2. Момент силы относительно данной оси не изменяется при переносе точки приложения силы в любую другую точку на линии её действия.
 |
Уравнения равновесия, для произвольно расположенной в пространстве системы сил, получаются из условий, что главный вектор и главный момент равны нулю, т.е. 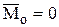 и
и 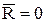 . Эти уравнения равновесия формулируются следующим образом: для равновесия произвольной пространственной системы сил необходимо и достаточно, чтобы суммы проекций сил на каждую из трех координатных осей и суммы моментов относительно этих осей были равны нулю.
. Эти уравнения равновесия формулируются следующим образом: для равновесия произвольной пространственной системы сил необходимо и достаточно, чтобы суммы проекций сил на каждую из трех координатных осей и суммы моментов относительно этих осей были равны нулю.
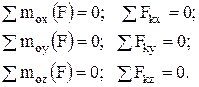
Контрольные вопросы:
1. Как Вы сформулируете понятие силы?
2. Что такое реакция связи?
3. Что такое проекция силы на ось?
4. Определить равнодействующую систему сходящихся сил?
5. Условия равновесия системы сходящихся сил.
6. Определить момент силы относительно точки?
7. Что такое пара сил и какими свойствами она обладает?
8. Указать формы условий равновесия плоской системы сил.
9. Каким образом решается задача на систему связанных тел?
10. Как определяется момент силы относительно оси?
11. Условия равновесия произвольной системы сил.
| <== предыдущая страница | | | следующая страница ==> |
| Система связанных тел | | | Кинематика точки |
Дата добавления: 2014-02-26; просмотров: 776; Нарушение авторских прав

Мы поможем в написании ваших работ!