
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Система связанных тел
Задача 3
Задача 2
Лестница АВ длиной 2а и весом Р опирается на гладкий горизонтальный пол и 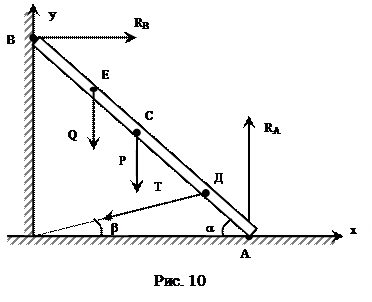 гладкую вертикальную стену, на которой в точке Е стоит человек весом Q. Чтобы лестница не скользила, она привязана к стене веревкой ОД. Определить реакции в точках А и В (стены и пола), а также натяжение веревки, если углы a и b, образуемые лестницей и веревкой с плоскостью пола известны и если расстояние
гладкую вертикальную стену, на которой в точке Е стоит человек весом Q. Чтобы лестница не скользила, она привязана к стене веревкой ОД. Определить реакции в точках А и В (стены и пола), а также натяжение веревки, если углы a и b, образуемые лестницей и веревкой с плоскостью пола известны и если расстояние 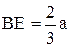 . Центр тяжести C лестницы находится в её середине (рис. 10).
. Центр тяжести C лестницы находится в её середине (рис. 10).
Решение: Используя принцип освобождаемости от связей, убираем связи, а их действие заменяем соответствующими реакциями. Составляем уравнения равновесия. Оси координат указаны на рис. 10.
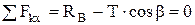 , (1)
, (1)
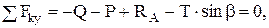 (2)
(2)
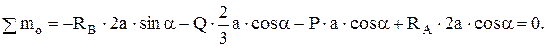 (3)
(3)
Из первого уравнения получаем: 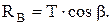
Из второго уравнения получаем: 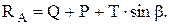
Подставляем значения для RA и RB в уравнение (3) и находим значение для
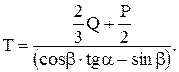
Определить опорные реакции в балочной конструкции, приведенной на
рис. 11, если Р=2 кН, q = 3 кН/м, m = 5 кНм. Размеры приведены на рис.11.
Решение: Используем принцип освобождаемости от связей, для чего вместо связей укажем их реакции (рис. 11, а). Указав оси координат для расчетной схемы, составляем уравнения равновесия. В данной задаче имеется три составляющих неизвестных опорных реакций, следовательно, необходимо составить три уравнения равновесия.


Рис. 11
Распределенная нагрузка, т.е. нагрузка приходящаяся на единицу длины, задается интенсивностью q= Н/см. Грузовая нагрузка, которая представляется как сосредоточенная сила равна Q=q∙ℓ, прикладывается в центре тяжести фигуры, образованной распределенной нагрузкой.
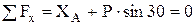 , (1)
, (1)
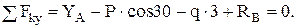 (2)
(2)
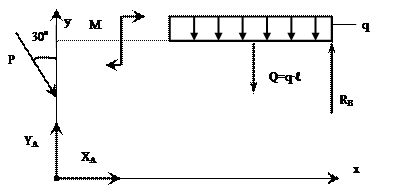

Рис. 11, а
При составлении третьего уравнения нужно учесть следующие два правила:
1. Момент от распределенной нагрузки равен, взятой с соответствующим знаком, площади грузовой нагрузки, умноженной на расстояние от центра тяжести грузовой нагрузки до рассматриваемой точки, относительно которой берется момент.
2. Если сила расположена под углом к координатным осям, то её необходимо разложить по проекциям на эти оси, а затем определять момент от каждой проекции в отдельности
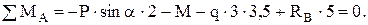 (3)
(3)
Момент следует брать относительно той точки, в которой сходятся большее количество неизвестных опорных реакций. Из полученных уравнений определяем неизвестные опорные реакции в следующем порядке:
из уравнения (3): 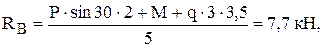
из уравнения (1): 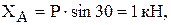
из уравнения (2): 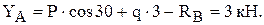
Следует отметить, что если при решении задач опорная реакция получилась со знаком минус, то, следовательно, её направление первоначально было выбрано неверно и его следует сменить на противоположное.
Во многих инженерных задачах приходится рассматривать равновесие не только одного тела, но и равновесие некоторой конструкции состоящей из нескольких тел. В этом случае приходится рассматривать равновесие каждого тела в отдельности, учитывая при этом силы, которыми действуют друг на друга тела, входящие в рассматриваемую систему. Тела могут быть соединены между собой с помощью шарнира, соприкасаться друг с другом и взаимодействовать одно с другим, вызывая определение силы взаимодействия. Эти силы, согласно аксиоме равенства действия и противодействия, всегда равны по модулю и противоположны по направлению.
Силы, с которыми тела, входящие в данную систему, действуют друг на друга, называются внутренними силами этой системы. Все остальные силы, включая сюда и реакции опор, называются внешними силами системы.
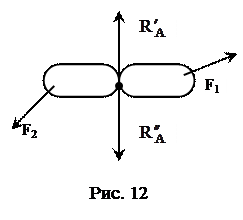
Если система находится в покое, то силы, приложенные к каждому из твердых тел, входящих в данную систему, уравновешиваются и, следовательно, для каждого из этих тел можно составить уравнения равновесия. В эти условия равновесия, для каждого тела в отдельности, войдут не только внешние силы, но и внутренние. Если же мы составляем уравнения равновесия для системы в целом, то внутренние силы, представляющие уравновешенную систему сил, в данные уравнения не войдут. Так для схемы, приведенной на рис. 12, 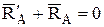 .
.
 При рассмотрении равновесия сил, приложенных к системе тел, можно мысленно расчленить систему на отдельные твердые тела, добавляя при этом к внешним силам, силы взаимодействия между телами (внутренние силы) и составлять соответственно уравнения равновесия для каждого тела. Учитывая при этом, что для равнодействующей внутренних сил неизвестен не только модуль, но и направление, их обычно представляют в виде двух составляющих, направленных по двум осям координат. Таким образом, для системы, состоящей из N тел, когда на каждое тело действует плоская система сил, можно составлять 3N уравнений равновесия и, следовательно, определять 3N неизвестных.
При рассмотрении равновесия сил, приложенных к системе тел, можно мысленно расчленить систему на отдельные твердые тела, добавляя при этом к внешним силам, силы взаимодействия между телами (внутренние силы) и составлять соответственно уравнения равновесия для каждого тела. Учитывая при этом, что для равнодействующей внутренних сил неизвестен не только модуль, но и направление, их обычно представляют в виде двух составляющих, направленных по двум осям координат. Таким образом, для системы, состоящей из N тел, когда на каждое тело действует плоская система сил, можно составлять 3N уравнений равновесия и, следовательно, определять 3N неизвестных.
| <== предыдущая страница | | | следующая страница ==> |
| ПЛОСКАЯ СИСТЕМА СИЛ | | | Произвольная система сил |
Дата добавления: 2014-02-26; просмотров: 660; Нарушение авторских прав

Мы поможем в написании ваших работ!