
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
ПЛОСКАЯ СИСТЕМА СИЛ
Задача 1
Однородная балка длины 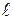 и веса Р удерживается в равновесии нитью ВС и шарниром А. Найти натяжение нити и реакцию шарнира А, если
и веса Р удерживается в равновесии нитью ВС и шарниром А. Найти натяжение нити и реакцию шарнира А, если 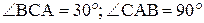 (рис. 7). Реакция нити ВС направлена по нити, а реакция шарнира А определяется в соответствии с теоремой о трех силах: если свободное твердое тело находится в равновесии под действием трех непараллельных сил, лежащих в одной плоскости, то линии действия этих сил пересекаются в одной точке. Заменив действие связей их реакциями, мы можем перейти от реальной схемы нагружения к расчетной (рис. 7, а). Учитывая, что сила Р приложена в середине балки и следовательно точка К (точка пересечения сил), делит отрезок ВС пополам, определим углы в полученной фигуре. Решение данной задачи может быть проведено двумя методами: геометрическим и аналитическим.
(рис. 7). Реакция нити ВС направлена по нити, а реакция шарнира А определяется в соответствии с теоремой о трех силах: если свободное твердое тело находится в равновесии под действием трех непараллельных сил, лежащих в одной плоскости, то линии действия этих сил пересекаются в одной точке. Заменив действие связей их реакциями, мы можем перейти от реальной схемы нагружения к расчетной (рис. 7, а). Учитывая, что сила Р приложена в середине балки и следовательно точка К (точка пересечения сил), делит отрезок ВС пополам, определим углы в полученной фигуре. Решение данной задачи может быть проведено двумя методами: геометрическим и аналитическим.
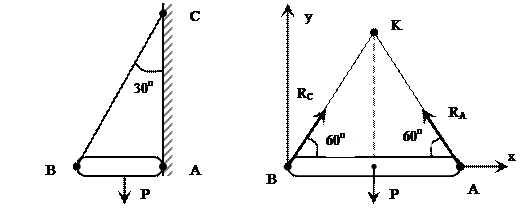

Рис. 7 Рис. 7, а
Геометрический метод.
Из сил, действующих на тело, строим силовой треугольник, который должен быть замкнутым, т.к. под действием этих сил тело находится в равновесии
(рис. 7, б). Для этого откладываем силы по известным направлениям, в любом выбранном масштабе.
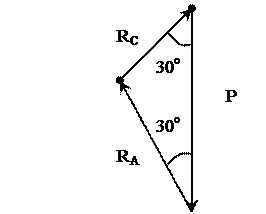 Таким образом, задача определения опорных реакций сводится к задаче решения полученного силового треугольника. Для решения воспользуемся теоремой синусов и составляем следующее соотношение:
Таким образом, задача определения опорных реакций сводится к задаче решения полученного силового треугольника. Для решения воспользуемся теоремой синусов и составляем следующее соотношение:
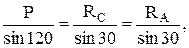
откуда получаем 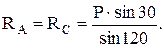
Рис. 7, б
Аналитический метод.
Для решения задачи составляются уравнения равновесия в виде суммы проекций всех сил на оси координат. Направления осей показаны на рис.7, а.
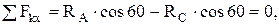 (1)
(1)
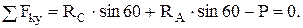 (2)
(2)
Из первого уравнения получаем RC =RA. Из второго находим 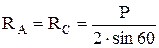 .
.
Плоской называется такая система сил, линии действий которых расположены в одной плоскости. При рассмотрении плоской системы сил введем определения для нагрузок. Парой сил называется система двух равных по модулю, параллельных и направленных в противоположные стороны сил, действующих на твердое тело
(рис. 8).
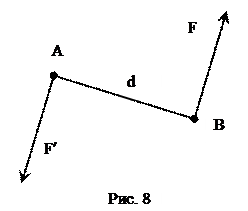 Плоскость, в которой расположена данная пара, называется плоскостью действия этой пары. Перпендикуляр, опущенный из точки приложения одной из сил на линию
Плоскость, в которой расположена данная пара, называется плоскостью действия этой пары. Перпендикуляр, опущенный из точки приложения одной из сил на линию
действия другой называется плечом пары (d). Действие пары сил определяется моментом пары. Численное значение момента пары определяется как произведение модуля одной из сил на плечо этой пары.
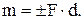
Приведем следующие два свойства пар сил:
1. Данную пару, не изменяя её действия на тело, можно переносить как угодно в плоскости её действия.
2. Не изменяя действия данной пары на тело, можно изменять модуль сил и плечо этой пары, сохраняя неизменным модуль и направление вращения пары.
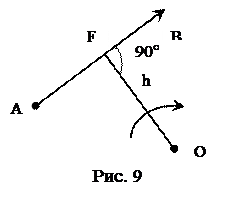 Другим важным понятием является момент силы относительно данной точки (рис. 9). Момент силы относительно данной точки равен произведению модуля силы на плечо, т.е. длину перпендикуляра, опущенного из этой точки на линию действия силы. Следовательно, будем иметь
Другим важным понятием является момент силы относительно данной точки (рис. 9). Момент силы относительно данной точки равен произведению модуля силы на плечо, т.е. длину перпендикуляра, опущенного из этой точки на линию действия силы. Следовательно, будем иметь
Mo(F)=±F∙h.
Момент силы считается положительным, если тело под действием данной силы стремится вращаться относительно точки О против часовой стрелки.
Отметим следующие свойства момента силы:
1. Момент силы относительно данной точки не изменяется при переносе точки приложения силы вдоль линии действия силы.
2. Момент силы относительно данной точки обращается в нуль в том случае, когда линия действия силы проходит через эту точку.
При решении задач на плоскую систему сил пользуются уравнениями равновесия. Для равновесия плоской системы сил необходимо и достаточно, чтобы сумма проекций этих сил на две координатные оси и сумма моментов относительно произвольно выбранной точки равнялись нулю
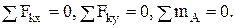
Существуют и две другие формы условий равновесия, но они используются гораздо реже.
Вторая форма условий равновесия: для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы суммы моментов этих сил относительно каких-нибудь двух центров А и В и сумма их проекций на ось, не перпендикулярную к прямой АВ, были равны нулю.
Третья форма: для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы суммы моментов всех этих сил относительной любых трех центров А, В и С, не лежащих на одной прямой, были равны нулю.
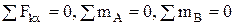 ;
;
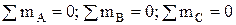 .
.
| <== предыдущая страница | | | следующая страница ==> |
| СИСТЕМА СХОДЯЩИХСЯ СИЛ | | | Система связанных тел |
Дата добавления: 2014-02-26; просмотров: 533; Нарушение авторских прав

Мы поможем в написании ваших работ!