Описание топологии физических связей

Разработка дискретной модели многомерного объекта

Построение математической модели объекта предусматривает последовательное выполнение двух этапов:

1. Описание топологии физических связей многомерного объекта управления;

2. Идентификация объекта по каналам управления и возмущения.

Структуры различных технологических объектов имеют существенные отличия и поэтому не могут быть описаны небольшим набором стандартизованных структурных схем. Однако реальные структуры можно привести к необходимой канонической форме, применяя правила преобразования схем.

На примере двумерного объекта (рис. 4.2) показаны две основные структуры взаимосвязей выходных параметров.

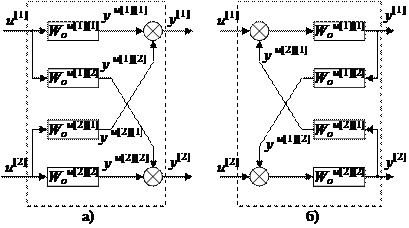
Рис. 4.2. Канонические структуры двумерного объекта:

а) P-каноническая структура; б) V-каноническая структура

Первый тип – P-каноническая структура, когда каждый входной сигнал действует на все выходные (рис. 4.2 а). При этом взаимосвязь параметров описывается векторно-матричным уравнением вида:

y=W_о^u·u, (4.1)

где y=[y^[1](z), y^[2](z)]^Т – вектор выходов ОУ; и=[и^[1](z), и^[2](z)]^Т – вектор управляющих воздействий; W_о^u – матрица дискретных передаточных функций объекта по основным и перекрестным каналам:

W_о^u=.

Если же каждый вход действует только на соответствующий выход, а каждый выход – на другие входы, то такие многомерные объекты относят к V-канонической структуре (рис. 4.2 б). Для V-канонической структуры модель объекта будет представлена векторно-матричным уравнением вида:

y=W_D^u·(u+W_П^u·y), (4.2)

или y=(I-W_D^u·W_П^u)^-1·W_D^u·u, (4.3)

где W_D^u, W_П^u – диагональная матрица, содержащая передаточные функции основных каналов, и матрица, получаемая из W_о^u заменой диагональных элементов нулями;

W_D^u=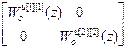; W_П^u=.

Однако, при необходимости, используя соответствующие преобразования, объект, имеющий V-каноническую структуру, можно представить эквивалентной P-структурой и наоборот.

Рассмотрим эквивалентное представление объекта с V-канонической структурой с помощью P-канонической структуры. Выражение (4.2) с учетом обозначения:

W_V^{u экв}=(I-W_D^u·W_П^u)^-1·W_D^u, (4.4)

примет вид:

y=W_V^{u экв}·u, (4.5)

где матрица W_V^{u экв} имеет следующую структуру:

W_V^{u экв}=.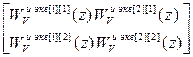

Из анализа (4.5) следует, что описываемый этим выражением объект имеет P-каноническую структуру (рис. 4.2 а), где вместо передаточных функций основных и перекрестных каналов в (4.1) используются соответствующие элементы матрицы W_V^{u экв}, получаемые из правой части уравнения (4.4).

Таким образом, переход от V-канонической структуры к P-канонической структуре заключается в расчете матрицы W_V^{u экв} и в дальнейшем использовании зависимости (4.5).

Для второго случая (переход от P-канонической структуры к V-канонической структуре) проведём преобразования, разложив матрицу W_о^u уравнения (4.1) на матрицу W_оD^u, содержащую только диагональные элементы, и матрицу W_оB^u, содержащую оставшиеся элементы:

y=W_о^u·u=(W_оD^u+W_оB^u)·u=W_оD^u·u+W_оB^u·u=

=W_оD^u·(u+(W_оD^u)^-1·W_оB^u·u)=W_оD^u·(u+(W_оD^u)^-1·W_оB^u·(W_о^u)^-1·y)=

=W_оD^u·(u+(W_оD^u)^-1·(W_о^u-W_оD^u)·(W_о^u)^-1·y)=

=W_оD^u·(u+((W_оD^u)^-1-(W_о^u)^-1)·y). (4.6)

Обозначив:

W_{P D}^{u экв}=W_оD^u, W_{P П}^{u экв}=(W_оD^u)^-1-(W_о^u)^-1, (4.7)

получим:

y=W_о^u·u=W_{P D}^{u экв}·(u+W_{P П}^{u экв}·y), (4.8)

или y=(I-W_{P D}^{u экв}·W_{P П}^{u экв})^-1·W_{P D}^{u экв}·u. (4.9)

Полученное уравнение (4.9) P-канонической структуры аналогично уравнению (4.3) V-канонической структуры.

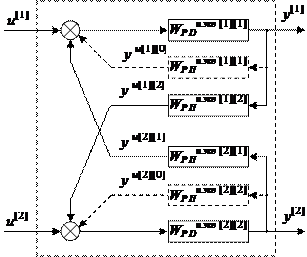
Анализ выражения (4.8) показывает, что объект (рис. 4.2 а) может быть представлен эквивалентной (рис. 4.2 в) V-канонической структурой аналогично (рис. 4.2 б), где вместо передаточных функций основных и перекрестных каналов используются соответствующие элементы матриц W_{P D}^{u экв} и W_{P П}^{u экв}. Однако при этом дополнительно возникают обратные связи по основным каналам, показанные пунктирной линией на рис. 4.2 в.

Рис. 4.2 в. Эквивалентная V-структура двумерного объекта

Наличие обратных связей W_{P П}^{u экв[1][1]} и W_{P П}^{u экв[2][2]} объясняется тем, что матрица W_{P П}^{u экв} не имеет нулевых диагональных элементов в отличие от матрицы W_П^u.

Для доказательства наличия обратных связей вычислим матрицы (W_оD^u)^-1, (W_о^u)^-1, а затем W_{P П}^{u экв}:

(W_оD^u)^-1==

=;

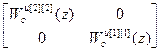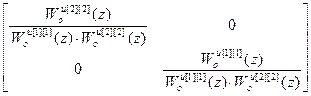(W_о^u)^-1=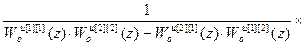

=

=

;

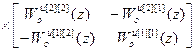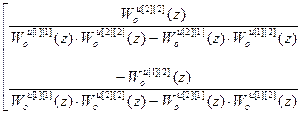
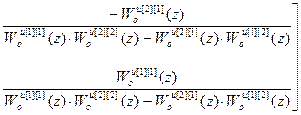W_{P П}^{u экв}=(W_оD^u)^-1-(W_о^u)^-1=

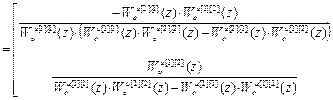
. (4.10)

Из (4.10) видно, что если основные и перекрестные каналы объекта имеют ненулевые передаточные функции и матрица W_о^u невырождена, то все элементы матрицы W_{P П}^{u экв} будут ненулевыми, включая диагональные. Это, исходя из (4.8), и приводит к появлению обратных связей по основным каналам (пунктирные линии на рис. 4.2 в).

Таким образом переход от P-структуры к V-структуре заключается в расчете матриц W_{P D}^{u экв} и W_{P П}^{u экв} и использовании зависимости (4.9).

В дальнейшем будем рассматривать P-канонические структуры многомерных объектов, как наиболее распространённые для большинства технологических процессов.

Среди всего многообразия форм дискретного математического описания непрерывных технологических объектов наиболее удобной для практического использования является параметрическая форма разностных уравнений. К форме разностных уравнений можно перейти от любой другой формы описания как дискретного вида, так и непрерывного (например, дифференциальной, дифференциально-интегральной или передаточных функций в операторном виде).

Рассмотрим типовой двумерный объект P-канонической структуры в условиях внешних контролируемых возмущений f ^[1], f ^[2] на управляемые параметры (рис. 4.3).

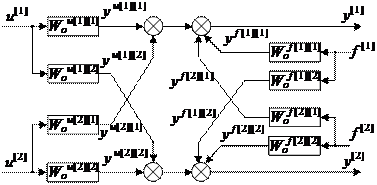
Рис. 4.3. Структурная схема двумерного объекта со связанными

параметрами и двумя возмущениями

Обобщённые структуры описывают только пути (топологию) передачи сигналов по каналам связи. Расчет же численных значений выходов основных, перекрестных и каналов возмущений, а также управляемых величин многомерных объектов в дискретной форме проводится на основе разностных уравнений или дискретных передаточных функций. При этом дискретная модель двумерного объекта описывается следующей системой разностных уравнений:

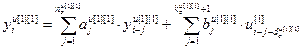, (4.11)

,

,

,

,

,

,

,

,

,

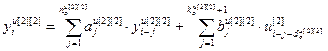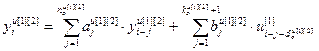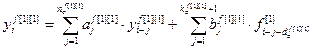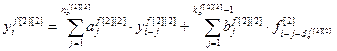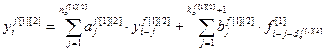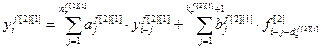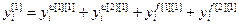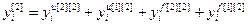или, применяя прямое преобразование с помощью оператора сдвига z, система разностных уравнений (4.11) с использованием дискретных передаточных функций запишется в виде:

y^u[k][j](z)=u^[k](z)·W_о^u[k][j](z),

y ^{f [h][j]}(z)=f ^[h](z)·W_о^{f [h][j]}(z), (4.12)

,

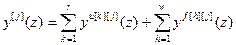где и^[k](z) – управляющее воздействие;

f ^[h](z) – внешнее контролируемое возмущение;

y^[j](z) – выход объекта;

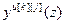– выход основного (k=j) или перекрестного (k≠j) канала ОУ;

– выход по каналу возмущения;

W_о^u[k][j](z)===

==

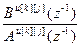
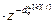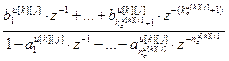
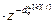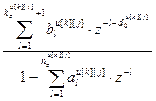=– дискретная передаточная функция по основному (k=j) или перекрестному (k≠j) каналу ОУ;

W_о^{f [h][j]}(z)===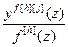

==

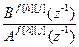
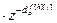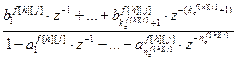
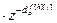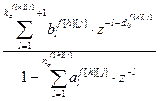=– дискретная передаточная функция по каналу возмущения;

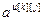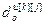, , – параметры и число тактов запаздывания дискретной передаточной функции канала ОУ, связывающего k-ый вход и j-ый выход;

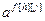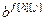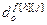, , – параметры и число тактов запаздывания дискретной передаточной функции по каналу возмущения, связывающего h-ый вход и j-ый выход;

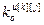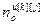, – порядки числителя и знаменателя дискретной передаточной функции по основному (k=j) или перекрестному (k≠j) каналу ОУ;

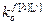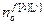, – порядки числителя и знаменателя дискретной передаточной функций по каналу возмущения;

A, B – обозначения полиномов; k, j=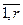(r=2); h=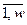(w=2); r – размерность объекта управления; w – число возмущающих воздействий; 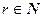; 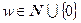, N – множество натуральных чисел.

Аналогично можно описать многомерный объект (рис. 4.1) с большим числом входных, выходных и возмущающих параметров с учётом внутренних взаимосвязей.

Описание каналов объекта исследования в форме передаточных функций с оператором сдвига z удобно применять в тех случаях, когда необходимо проводить свёртку и преобразование структурных схем (при выводе алгоритмов компенсаторов внешних возмущений, компенсаторов перекрёстных связей и т.д.).

Переход от одной формы описания к другой и обратно не вызывает больших трудностей и может быть широко использован в дальнейшем при синтезе многомерных систем управления.

Дата добавления: 2014-03-11; просмотров: 499; Нарушение авторских прав

Мы поможем в написании ваших работ!