Разработка алгоритмов синтеза управляющей части цифровой системы

Идентификация объекта по каналам управления и возмущения

Векторно-матричная форма описания многомерного объекта

Для случая r-мерного объекта управления, подверженного влиянию произвольного числа w внешних воздействий (рис. 4.4), модель в разностной форме можно описать системой уравнений (4.13).

Рис. 4.4. Структурная схема r-мерного объекта со связанными

параметрами подверженного влиянию произвольного числа w

внешних контролируемых возмущений

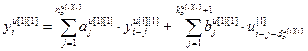, (4.13)

,

,

,

,

,

,

,

,

.

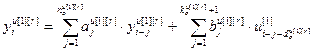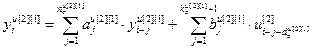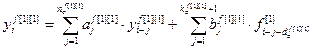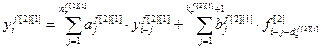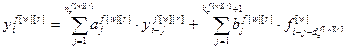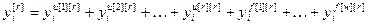Отсюда получим общую рекуррентную формулу для любого основного (k=j) или перекрестного (k≠j) каналов ():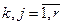

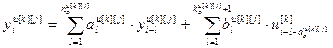. (4.14)

Для каналов возмущений:

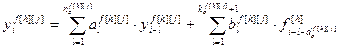, (4.15)

где .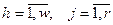

Суммарный измеряемый сигнал объекта по каждому выходу будет определяться суммой сигналов по основному, соответствующим перекрестным и возмущающим каналам:

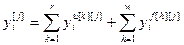, . (4.16)

Ввиду громоздкой записи модели многомерного объекта в скалярной форме (4.14) – (4.16), ее использование затруднительно для решения последующих задач синтеза цифровой системы оптимального управления. Поэтому дискретную модель объекта представим в векторно-матричной форме:

=,

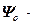
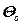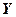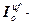
=, (4.17)

где =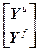, 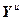=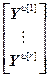, 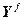=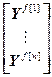– блочные векторы;

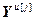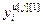=[,…,]^Т – вектор выходов основных и перекрестных каналов, связывающих j-ое управляющее воздействие со всеми управляемыми величинами; ;

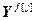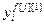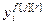=[,…,]^Т – вектор выходов каналов возмущений, связывающих j-ое возмущающее воздействие со всеми управляемыми величинами; j=;

=, =,

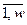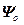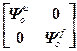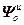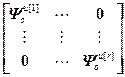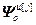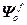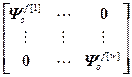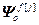=, =, =– блочные матрицы;

=[,...,,...,]

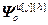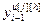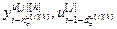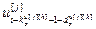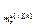
– матрица-строка переменных состояния основного или перекрестного каналов, связывающих j-ое управляющее воздействие и h-ую управляемую величину; ;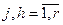

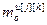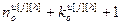=– число переменных состояния основных и перекрестных каналов;

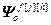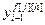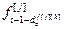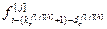=[,...,,,...,] – матрица-строка переменных состояния по каналу возмущения, связывающего j-ое внешнее воздействие и h-ый выход объекта, ; , ;

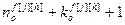=– число переменных состояния каналов возмущений;

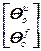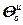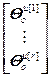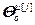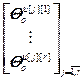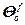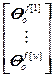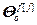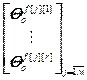=, =, =, =, =– блочные векторы;

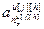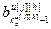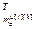=[,…,,,…,]– вектор параметров модели основного или перекрестного каналов, связывающего j-ое управляющее воздействие и h-ую управляемую величину; ;

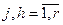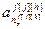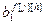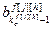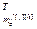=[,…,,,…,]– вектор параметров дискретной модели канала возмущения относительно j-го внешнего воздействия и h-го выхода объекта; , ;

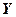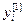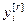=[,…,]^Т – вектор управляемых величин объекта;

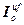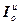
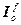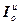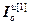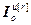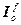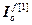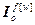=[], =[,…,], =[,…,] – блочные матрицы-строки;

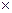(), () – единичные матрицы, rr.

Разработанная структура модели r-мерного объекта управления при наличии w возмущающих воздействий позволяет автоматизировать этап составления дискретного динамического описания технологического процесса независимо от внутренней структуры взаимосвязей технологических параметров и их количества.

В каждом конкретном случае достаточно указывать размерность объекта управления по входам, выходам и возмущениям, а также структуру связей между ними с помощью введенной индексации, после чего переходят к выполнению второго этапа разработки математической модели объекта управления – идентификации каналов управления и возмущения.

Основой математического аппарата синтеза ЦСУ являются разностные схемы [7]. При этом каждый из каналов ОУ описывается разностным уравнением, которое с учетов векторной формы записи может быть представлено в следующем виде:

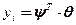(4.18)

где u_i, y_i – вход и выход ОУ;

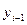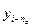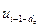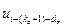=[,…,,,…,]– вектор переменных состояния;

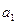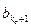=[,…,,,…,]– вектор параметров разностного уравнения;

d_о=τ_о /T'₀ – целое число тактов запаздывания;

τ_о – время запаздывания;

T'₀ – такт квантования;

n_о, k_о – порядки знаменателей и числителей дискретных передаточных функций каналов ОУ (n_о≥k_о);

m_о=n_о+k_о+1 – число переменных состояния каналов ОУ;

i – индекс такта квантования.

Широко применяемым для идентификации линейных и нелинейных объектов (систем) является метод наименьших квадратов (МНК), позволяющий обеспечить высокую адекватность получаемых моделей. Суть его заключается в нахождении таких параметров модели, при которых сумма квадратичных отклонений между экспериментальными значениями выхода объекта и рассчитанными по модели была минимальной:

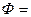
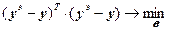, (4.19)

где 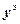=[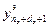,…,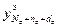]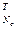– вектор экспериментальных значений выхода ОУ, полученных путем измерения через равные промежутки времени T'₀ при снятии кривой разгона; 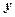=[,…,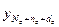]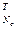– вектор значений выхода ОУ, рассчитанных по модели (4.18);

N_о – объем выборки при идентификации.

Поскольку вектор 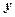, с учетом (4.18), может быть представлен соотношением:

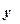=, (4.20)

то (4.19) примет вид:

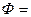
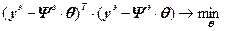, (4.21)

где 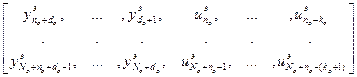– матрица экспериментальных значений, N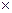_оm_о.

Так как квадратичная функция 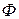относительно вектора неизвестных параметров ограничена снизу, то точка минимума существует и является решением системы линейных уравнений:

2·или 2·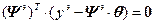, (4.22)

где 0=[0,…,0]– нулевой вектор.

Если матрица (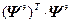) не вырождена, то решение единственно. Необходимое условие для выполнения данного требования – входной сигнал представляет собой возбуждающий процесс порядка не ниже n_о, т.е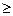. N_оn_о.

Выполнив преобразования, приведем уравнения (4.22) к нормальному виду:

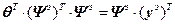или

. (4.23)

Решая нормализованное уравнение (4.23), или соответствующую систему линейных уравнений (например, методом Гаусса), можно найти параметры (коэффициенты) разностного уравнения (4.18).

В векторно-матричной форме решение имеет вид:

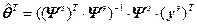или

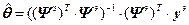, (4.24)

где 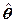=[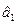,…,,,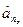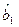…,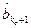]– вектор оценок неизвестных параметров.

Полученные таким образом оценки параметров 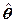с помощью МНК не смещены (М(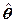)=), эффективны (=diag[(-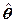) (-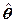)^Т]→min) и состоятельны, поскольку 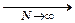0.

Оптимальная с точки зрения минимума среднеквадратичной ошибки оценка выходной переменной y_i записывается в виде:

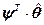=. (4.25)

Расчет параметров a_j (j=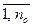), b_l (l=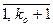) удобнее проводить не в абсолютных значениях, а в приращениях (вариациях), т.е. значение входа и выхода в установившемся состоянии перед нанесением входного воздействия (до начала эксперимента) принимаются равными нулю. После начала эксперимента, когда на вход подано воздействие, значение входа и выхода определяются как приращения.

Адекватность дискретных моделей различных порядков определяется по критерию Фишера. При отсутствии параллельных опытов модель адекватна ОУ, если расчетный критерий Фишера F_р больше критического значения F_табл(p, f₁, f₂):

F_р>F_табл(p, f₁, f₂), (4.26)

а при наличии параллельных опытов, если расчетный критерий Фишера F_р^пар меньше критического значения (p, f₁, f₂):

F_р^пар<(p, f₁, f₂). (4.27)

Критическое значение Фишера выбирается из таблиц распределения Фишера при выбранном уровне значимости.

В результате идентификации определяются порядки n_о, k_о и значения параметров a_j ( j=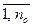), b_l (l=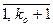) разностных уравнений (моделей) каналов ОУ, которые используются на этапе синтеза управляющей части системы и исследования.

Задача синтеза системы управления состоит в определении ее структуры и расчете настроек регуляторов и компенсаторов на основе априорной информации о динамике объекта, обеспечивающих заданные статические и динамические свойства системы.

Простейшим видом многосвязных систем можно считать системы несвязанного управления, которые проще при синтезе, настройке и эксплуатации и реализуемы даже в тех случаях, когда системы связанного управления технически неосуществимы [11] (например, автономные). Однако они восприимчивы к возмущениям, распространяющимся по основным и перекрестным каналам. При этом в системах с сильными внутренними связями область устойчивого управления резко сокращается. Если при расчете оптимальных настроек регуляторов такой системы не учитывать влияние перекрестных каналов, то она будет неустойчивой. Для сохранения устойчивости несвязанной системы приходится уменьшать коэффициенты усиления регуляторов, значительно снижая скорость их действия, что резко ухудшает качество управления.

Как ранее было сказано при сильных внутренних связях возможность получить высокое качество управления нужно искать не корректируя настройку не связанных между собой регуляторов, а развязывая внутренние связи по перекрестным каналам путем создания систем связанного управления, вводя дополнительные внешние компенсирующие связи между регуляторами. Накладывать эти связи можно в различных местах: между входами или выходами регуляторов или непосредственно между регулирующими органами; могут применяться смешанные связи и т.д.

Теоретической основой для разработки рациональных схем связанного управления является принцип автономности, предложенный И.Н. Вознесенским в 1934 г.: вводя внешние компенсирующие связи между регуляторами, можно добиться расчленения сложной системы со многими взаимосвязанными параметрами на ряд простейших сепаратных систем, обладающих одним управляемым параметром каждая. В результате теоретически может быть достигнута полная компенсация внутренних динамических связей между выходами. В этом случае изменение одного управляемого параметра не вызывает изменения остальных, если другие источники возмущающих воздействий стабилизированы. Однако автономные системы имеют ряд недостатков [12] (в частности они не всегда технически реализуемы).

Исходя из сказанного, рассмотрим два основных подхода к расчету управляющей части при синтезе многомерных систем с перекрестными связями:

1. На основе использования принципа автономности. При этом предварительно рассчитываются компенсаторы, после чего выполняется одновременная оптимизация всех основных регуляторов в связанной системе управления;

2. Одновременная оптимизация регуляторов и компенсаторов системы без использования принципа автономности (например, одним из численных методов) при учете влияния всех регулируемых величин и их взаимной связи.

При первом подходе расчет регуляторов может быть выполнен одним из двух вариантов:

1.1. Оптимизация всех основных регуляторов в связанной системе управления по моделям основных и перекрестных каналов многомерного объекта;

1.2. Оптимизация основных регуляторов в одноконтурных системах управления по моделям соответствующих эквивалентных объектов на основе декомпозиции связанной системы: представление сложной системы в виде совокупности сепаратных одноконтурных с одним регулируемым параметром, включающих соответствующие регулятор и эквивалентный объект.

Синтез многомерных систем невозможно рассматривать изолировано от внешних условий, проявляющихся в виде возмущающих факторов. Поэтому необходимо учитывать их влияние на управляемые величины введением компенсирующих воздействий с целью стабилизации или целенаправленного изменения управляемых координат.

Одним из способов, снижающих это влияние, является наличие самой обратной связи. Однако замкнутые системы не препятствуют проникновению в ОУ внешних возмущений, а только реагируют на их последствия; в результате закон изменения задания точно не выполняется.

В этом случае получить наилучшее качество управления объектом позволяет синтез и использование связно-комбинированных цифровых систем управления (СКЦСУ), существенно снижающих, а иногда и полностью исключающих влияние на выходную величину не только перекрестных каналов, но и внешних возмущений за счет применения соответствующих компенсаторов. При этом разработка наиболее эффективных систем этого класса связана с расчетом компенсаторов возмущений на основе принципа инвариантности, предложенного в 1938 г. Щипановым Г.В. Однако, наличие ряда недостатков [41,45], ограничивающих техническую реализацию инвариантных компенсаторов и, следовательно, систем, позволяет сформулировать следующие подходы к их синтезу:

1. Синтез компенсаторов на основе использования принципа инвариантности;

2. Оптимизация компенсаторов возмущения системы одним из численных методов.

Далее рассмотрим подробное описание указанных подходов и вариантов синтеза и расчет управляющих частей связанных и связно-комбинированных ЦСУ.

Дата добавления: 2014-03-11; просмотров: 585; Нарушение авторских прав

Мы поможем в написании ваших работ!