
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Функция распределения двумерной случайной величины и ее свойства
Определение. Функцией распределения двумерной случайной величины (X,Y) называется функция 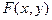 , определенная для каждой пары чисел (x,y). Вероятность того, что Х примет значение меньше х и при этом Y примет значение меньше y.
, определенная для каждой пары чисел (x,y). Вероятность того, что Х примет значение меньше х и при этом Y примет значение меньше y.
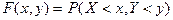
Геометрически это раввенство можно истолковать так: 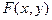 есть вероятность того, что случайная точка (x,y) попадает в бесконечный квадрат с вершиной в точке (x,y), расположенный левее и ниже этой вершины (рис.12.1.).
есть вероятность того, что случайная точка (x,y) попадает в бесконечный квадрат с вершиной в точке (x,y), расположенный левее и ниже этой вершины (рис.12.1.).
 |
Пример.Найти вероятность того, что в результате испытаний составляющая Х двумерной случпйной величины (X,Y) примет значение меньше 2-х, и при этом составляющая Y примет значение меньше 3-х, если известно, что 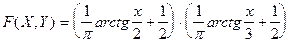 .
.
По определению, 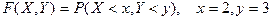 . Получим: вероятность
. Получим: вероятность 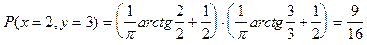 .
.
Свойство 1. Значение функции распределения удовлетворяет двойному неравенству 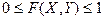 .
.
Свойство 2. Функция распределения 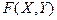 есть неубывающая функция по каждому аргументу, т.е.
есть неубывающая функция по каждому аргументу, т.е. 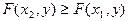 . Если
. Если 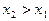 , и
, и 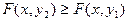 и если
и если 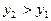 .
.
Свойство 3. Имеет место предельное соотношение
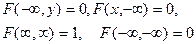
Свойство 4. При 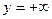 , функция распределения системы становится функцией распределения составляющей х:
, функция распределения системы становится функцией распределения составляющей х: 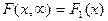 . Аналогично при
. Аналогично при 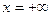
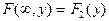 .
.
| <== предыдущая страница | | | следующая страница ==> |
| Общие понятия | | | Плотность совместного распределения вероятностей непрерывной двумерной случайной величины (двумерная плотность вероятности). Ее свойства |
Дата добавления: 2014-02-26; просмотров: 1133; Нарушение авторских прав

Мы поможем в написании ваших работ!