
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ВОЛНОВОГО ДВИЖЕНИЯ
Отвлечемся временно от описания строения атомов, чтобы познакомиться с математическим описанием волнового движения. Рассмотрим волну, изображенную на рисунке, которая с
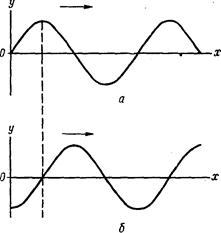
течением времени передвигается вдоль оси х в направлении, указанном стрелкой. Это волновое движение можно описать количественно с помощью дифференциального уравнения
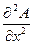 = (
= (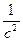 ) (
) (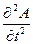 ),
),
где А — амплитуда, т. е. высота волны, измеряемая по оси у при данном расстоянии х; с — скорость, с которой передвигается волна, a t— время. Решением этого дифференциального уравнения является функция
A==а sin2p(х/l—nt).
где l— длина волны, n—ee частота и а—постоянная. Из уравнения можно найти амплитуду А во время t в положении х.
Другой тип волнового движения — стоячая волна — возникает при колебаниях струны с закрепленными концами. Стоячей волне отвечает стационарная картина с фиксированным профилем (вместо перемещающегося вдоль оси х, как в случае волны, изображенной ранее). Эмпирическим .путем
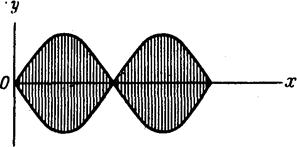
было найдено, что такая модель, обобщенная на случай трехмерной волны, лучше описывает поведение электрона, связанного с ядром. Дифференциальное уравнение, описывающее такую одномерную стоячую волну, имеет следующее решение:
A==2asin(2pх/l)cos2pnt,
или более просто
A=f(x)cos2pnt,
где f(x)—сокращенная запись для 2a sin(2px/l)—функция только координаты х.
Вторая производная функция по времени, будучи подставленной в уравнение , позволяет исключить величину t.
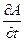 = -2a sin(2p
= -2a sin(2p ) sin2pnt×2pn
) sin2pnt×2pn
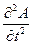 = -2a sin(2p
= -2a sin(2p ) cos2pnt×4p2n2
) cos2pnt×4p2n2
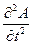 = -A4p2n2 n=
= -A4p2n2 n= 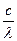
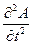 = -A
= -A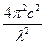 = c2
= c2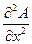
Получающееся уравнение для стоячей волны может быть обобщено для описания трехмерной волны:
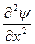 +
+ 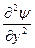 +
+ 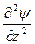 + 4p2y/l2 == 0,
+ 4p2y/l2 == 0,
где y—трехмерный аналог величины А ). Введя сокращенное обозначение,
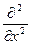 +
+ 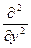 +
+  = Ñ2,
= Ñ2,
получаем
Ñ2y+4p2y/l2=0. )
Уравнения являются дифференциальными уравнениями, описывающими стационарную трехмерную волну, и не содержат переменной t. Целью исключения этой переменной было получение уравнения, решения которого не зависят от времени.
| <== предыдущая страница | | | следующая страница ==> |
| ВОЛНОВЫЕ СВОЙСТВА ЭЛЕКТРОНОВ | | | РЕШЕНИЕ УРАВНЕНИЯ ШРЕДИНГЕРА |
Дата добавления: 2014-03-11; просмотров: 523; Нарушение авторских прав

Мы поможем в написании ваших работ!