РЕШЕНИЕ УРАВНЕНИЯ ШРЕДИНГЕРА

УРАВНЕНИЕ ШРЕДИНГЕРА

Шрёдингер выбрал математическое описание стоячей волны в качестве модели для строения атома. Он включил в выражение для стоячей волны предположение де Бройля l=h/mJ и получил

Ѳy + (4p²m²J²/h²)y == 0.

Комбинируя уравнения с уравнением , связывающее полную энергию Е, потенциальную энергию V и кинетическую энергию mJ²/2 .

Е = V + mJ²/2 или J² = 2 (Е — V)/m,

можно получить уравнение Шрёдингера в его обычной форме

Ѳy +(8p²m/h²)(E-V)=0

Следует помнить, что уравнение Шредингера не выводится из более общих законов, а является следствием, во-первых, эмпирического выбора уравнения для стоячей волны в качестве модели для описания поведения -электрона в атоме и, во-вторых, включения в последнее гипотезы де Бройля. Обоснованием такого «вывода» является тот факт, что решение уравнения приводит к значениям энергии Е, точно соответствующим найденным экспериментально из атомных спектров

Остановимся на смысле символа y в уравнении Шредингера. Поскольку y является трехмерным аналогом А (амплитуды плоской волны), y рассматривается как амплитудная функция. Самой функции y нельзя приписать физический смысл, но такой смысл имеет величина yy*, которая, как можно показать, пропорциональна вероятности нахожденияэлектрона в данном положении (y* — это функция, комплексносопряженная с y). Величина yy^*dt передает вероятность нахождения электрона в элементе объема dt. Если y является действительной функцией, yy* переходит в y².

Рассмотрим теперь качественно метод, используемый для решения уравнения Шредингера для случая атома водорода. Первым шагом является упрощение решения путем преобразования уравнения от декартовых координат (оси х, у и z) к сферическим полярным координатам.

При преобразовании системы координат уравнение Шредингера переходит в уравнение

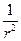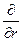()()(r²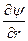) + ()(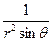)(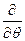sinq) +

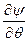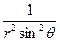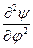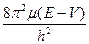. +()() + )y = 0

Здесь m — приведенная масса ' m = ,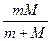

где М—масса ядра, m—масса электрона.

Уравнение можно разделить на более простые уравнения, каждое из которых включает только одну переменную r, q или j и может быть решено независимо. Эти уравнения имеют бесконечное множество решений; но, для того чтобы решения имели смысл для описания поведения электрона в атоме, они должны удовлетворять изложенным ниже требованиям «а» — «в». Каждое возможное решение представляет собой волновую функцию y, описывающую орбиталь — состояние атома. Для выделения пригодных решений из бесконечного общего числа их нужно отобрать те, точки, что удовлетворяют следующим условиям:

а) волновая функция должна быть конечной и непрерывной т. е. она не должна обращаться в бесконечность ни при каких значениях r, q и j .

б) решение должно быть однозначным, т. е. в любой данной точке амплитуда может иметь только одно значение, а не несколько;

в) решения должны быть нормированы; это условие требует, чтобы взятый по всему пространству интеграл от функции (являющейся решением), возведенной в квадрат и умноженной на dt, был равен единице, т. е.

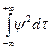=1

Поскольку y²dt связано с вероятностью нахождения электрона в элементе объема dt, интегрирование в уравнении просто требует, чтобы вероятность нахождения электрона где-либо в пространстве была равна единице.

Для неионизированного атома имеется лишь ограниченное число решений уравнения Шрёдингера, удовлетворяющих всем сформулированным выше требованиям. Такие дозволенные решения называются собственными функциями, и каждое из них описывает состояние — орбиталь, на которой в атоме могут находиться два электрона Орбитали отличаются нижними индексами при y; каждая орбиталь однозначно определяется набором квантовых чисел n ,l и m, где n соответствует основному номеру оболочки Уравнения для y_np разделяются на радиальную часть y_r (зависящую от расстояния г) и угловую часть y_qj (являющуюся функцией углов q и j). Полная волновая функция представляет собой просто произведение этих двух частей, т. е. y=y_qjy_r.Выражения для s-орбиталей не включают никакой зависимости от углов, и поэтому они обладают сферической симметрией. Число решений указывает, сколько существует орбиталей с данной энергией (т. е. в данной оболочке с одним главным квантовым числом). Для орбитали, отвечающей оболочке с n=1 (т.е. оболочке с самой низшей энергией), возможно только одно решение y_1s. Для значений энергии, соответствующих n=2, имеются два очень близких энергетических уровня , соответствующих волновым функциям y_2s и y_2p. Есть только одно решение для y_2s и три решения для y_2p, соответствующие трем орбиталям y_2p0,y_2p+1,y_2p-1. Эти три 2р-орбитали имеют все одинаковую энергию. Для описания равенства энергий трех орбиталей используется термин«триждывырожденные». Для энергий, отвечающих оболочке с п=3, имеется девять решений, соответствующих одной y_3s-орбитали, трем вырожденным y_3p-орбиталям и пяти вырожденным y_sd-орбиталям. Решений, которые отвечали бы орбиталям y_1p или y_2d, нет, и таких орбиталей нет. Таким образом, выбрав в качестве модели стоячую волну, включив в волновое уравнение гипотезу де Бройля и отобрав физически приемлемые решения получившегося уравнения, можно сосчитать число возможных орбиталей в атоме водорода.

Дата добавления: 2014-03-11; просмотров: 620; Нарушение авторских прав

Мы поможем в написании ваших работ!