
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
ПЕРЕХОДНЫХ ПРОЦЕССОВ
ОБЩАЯ ХАРАКТЕРИСТИКА МЕТОДА АНАЛИЗА
НУЛЕВЫЕ И НЕНУЛЕВЫЕ НАЧАЛЬНЫЕ УСЛОВИЯ
Напряжение и заряд на емкостном элементе непосредственно после коммутации uc(0+) сохраняет те значения, которые он имел непосредственно до коммутации uc(0-) и далее изменяется с этих значений.
ВТОРОЙ ЗАКОН КОММУТАЦИИ
ПЕРВЫЙ ЗАКОН КОММУТАЦИИ
Переходным процессом называется процесс перехода от одного установившегося состояния электрической цепи к другому установившемуся состоянию.
Лекция №3 ПЕРЕХОДНЫЕ ПРОЦЕССЫ
Переходные процессы возникают в электрических цепях, содержащих реактивные элементы.
Ток и магнитный поток на индуктивном элементе непосредственно после коммутацииiL(0+) сохраняет те значения, которые он имел непосредственно до коммутации iL(0-) и далее изменяется с этих значений.
iL(0+) = iL(0) = iL(0-)
Время t(0-) представляет собой время, непосредственно до коммутации.
t(0) - момент коммутации.
t(0+) - это время, непосредственно после коммутации.
Этот закон показывает невозможность скачка тока через индуктивность.
ис(0+) = ис(0) = ис(0-)
Этот закон доказывает невозможность скачка напряжения на емкости.
НАЧАЛЬНЫЕ ЗНАЧЕНИЯ ВЕЛИЧИН.
Докоммутационными начальными значениями
называют значения токов, напряжений, непосредственно до
коммутации (при t=0-).
Послекоммутационными начальными значениями -значения токов и напряжений непосредственно после коммутации (при t=0+).
НЕЗАВИСИМЫЕ И ЗАВИСИМЫЕ НАЧАЛЬНЫЕ УСЛОВИЯ.
Значения токов через индуктивность iL(0-) и напряжений на емкостях uc(0), известные из докоммутационного режима, называются независимыми начальными условиями
Значения остальных токов и напряжений при t=0+ в послекоммутационной схеме, определяемые по независимым начальным значениям из законов Кирхгофа, и называются зависимыми начальными значениями.
Если к началу переходного процесса непосредственно перед коммутацией все токи и напряжения на пассивных элементах схемы равны нулю, то в схеме имеют место нулевые начальные условия,
если же к началу переходного процесса токи и напряжения в схеме не равны нулю, то в схеме имеют место ненулевые начальные условия.
Широко распространенными являются следующие методы расчета:
1. Классический метод
2. Операторный метод
3. Метод расчета путем применения интеграла Дюамеля.
РАСЧЕТ СОСТОИТ ИЗ СЛЕДУЮЩИХ ОСНОВНЫХ ОПЕРАЦИЙ
а) выбора положительных направлений токов в ветвях цепи;
б) определения значения токов и напряжений
непосредственно до коммутации;
в) составление характеристического уравнения
и определения его корней;
г) получения выражений для искомых токов и
напряжений как функций времени.
КЛАССИЧЕСКИЙ МЕТОД РАСЧЕТА
Переходной процесс в любой линейной цепи условно разбивается на свободный и принужденный
i= iсв + iпр где iсв , uсв – свободная составляющая
переходного тока,
u= uсв + uпр iпр , uпр – принужденная составляю-
щая тока или напряжения,
i, u – переходные значения тока или
напряжения в функции времени.
Составляется характеристическое уравнение цепи как выражения для входного сопротивления цепи переменному току, где jω заменяется через р, где р – корень характеристического уравнения
| Входное сопротивление будет равно: |
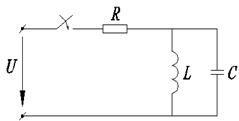
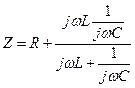
РИС 3.
Заменим jω → р. Характеристическое уравнение запишется в следующем виде
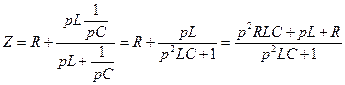
Чтобы определить корни характеристического уравнения его приравнивают к нулю и решают относительно р, Z(p)=0
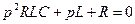
т. к данное уравнение второго порядка то и корней будет два:
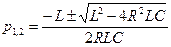
свободная составляющая переходного тока или напряжения записывается в виде показательной функции
iсв = Ae pt, где А - постоянная интегрирования
определяется из начальных условий при t =0
i(0) = iсв(0) + iпр(0),
р – корень характеристического уравнения.
Принужденная составляющая тока или напряжения определяется для установившегося послекоммутационного режима. Это значение тока или напряжения после затухания всех переходных процессов, определяется любым доступным методом.
Любой переходной процесс в линейной электрической цепи теоретически длится бесконечно, т.к. Ae pt никогда не будет равно нулю. Но после определенного промежутка времени свободной составляющей переходного процесса можно пренебречь.
Этот промежуток ограничивается 5 τ, где τ - это постоянная времени, в течение которого первоначальное значения функции уменьшается в "е" раз.

- это величина обратная корню характеристического уравнения.
Преимуществом классического метода является его наглядность: при расчете цепи ясно виден характер изменения всех токов и напряжений.
Недостаток метода - необходимость решения как системы дифференциальных уравнений для определения всех токов и напряжений цепи, так и системы алгебраических уравнений для определения постоянных интегрирования. Этого недостатка лишен операторный метод расчета.
ОПЕРАТОРНЫЙ МЕТОД РАСЧЕТА
Операторный метод расчета переходных процессов основан на замене функций времени (оригинала ) f(t) - функцией некоего комплексного переменного р, т.е. его изображением F(p) с помощью преобразования Лапласа.
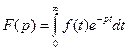
переход от оригинала к изображению с помощью прямого преобразования Лапласа.
Или f(t)  F(P), где
F(P), где  знак соответствия.
знак соответствия.
Операторный метод позволяет свести операцию дифференцирования к умножению, а операцию интегрирования - к делению. Это облегчает интегрирование дифференциальных уравнений.
Таблица 1.
Изображения некоторых простейших функций.
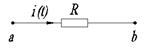
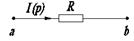
| Исходная схема | Операторная схема замещения |
Активное сопротивление
|
|
Индуктивное сопротивление
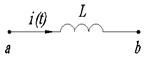
|
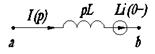
|
Емкостное сопротивление
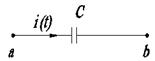
|
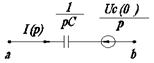
|
Здесь iL(0-) и iL(0) соответственно ток в катушке и напряжение на конденсаторе в момент коммутации. Таким образом, операторный метод позволяет учесть начальные условия автоматически, поэтому отпадает необходимость решения системы алгебраических уравнений для определения постоянных интегрирования.
| <== предыдущая страница | | | следующая страница ==> |
| Графические методы расчета | | | Переход от изображения к оригиналу |
Дата добавления: 2014-03-11; просмотров: 491; Нарушение авторских прав

Мы поможем в написании ваших работ!