Переход от изображения к оригиналу

Закон Ома в операторной форме

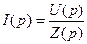- изображение тока в цепи.

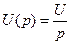- изображение постоянного напряжения.

Характеристическое (операторное) сопротивление Z ( р) для цепи (рис.3)

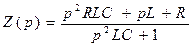
Тогда

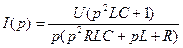
Операцию перехода от изображений к функциям времени можно осуществить двумя путями:

а) с помощью обратного преобразования Лапласа,

б) применением теоремы разложения.
Наиболее распространен 2-ой метод.

Переход от изображения I(р) к функции времени i (t) производят с помощью формулы разложения:

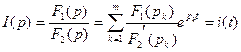
изображение оригинал

Число слагаемых в этой формуле равно числу корней характеристического уравнения р_к.

Если хотя бы один из корней характеристического уравнения имеет нулевые значения, значит в этой цепи присутствует принужденная составляющая т.к. е⁰=1.

Дата добавления: 2014-03-11; просмотров: 490; Нарушение авторских прав

Мы поможем в написании ваших работ!