Площадь плоской фигуры

Некоторые применения определённого интеграла

Площадь под кривой

В соответствии с геометрическим содержанием определённого интеграла площадь криволинейной трапеции, ограниченной кривой f(x) ≥ 0, прямыми х = а, х = b и интервалом [a,b], определяется величиной

Площадь криволинейного сектора между полярными радиусами α и β определяется формулой

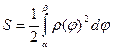
Если кривая задана функциями x(t) и y(t), то площадь фигуры под этой кривой в границах х = t₁, х = t₂ на интервале [t_1, t₂] определяется интегралом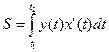

Задача. Вычислить площадь плоской фигуры, ограниченной аркой циклоиды x = t-sin(t), y = 1-cos(t) и осью ОХ.

Решение:

>> syms t

>> x=(t-sin(t));

>> y=(1-cos(t));

>> tn=0:pi/100:2*pi;

>> s=int(y*diff(x,t),t,0,2*pi)

s =3*pi

Построение площади

>> xp=subs(x,t,tn);

>> yp=subs(y,t,tn);

>>C=[0.9 0.9 0.9]; % оттенки черного (>> patch(xp,yp,'r') закрашивает площадь фигуры красным или любым другим цветом

>> patch(xp,yp,C)

>> ezplot(x,y) % построение линии заданной параметрически

Площадь между кривыми

Площадь, ограниченная линиями у₁(х), у₂(х), х = а, х = b, определяется абсолютной величиной определённого интеграла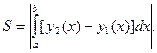

Задача: Найти площадь фигуры, ограниченной параболой у₁=(х-1)² и ветвью гиперболы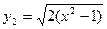

Решение:

y1=(x-1)^2;y2=(2*(x^2-1))^(1/2);

>> x0=solve(y2-y1)

x0 =[ -i][ 1][ 3]

>> S=int(y2-y1,x,1,3)

S =10/3-1/2*log(3*2^(1/2)+4)*2^(1/2)+1/4*log(2)*2^(1/2)

>> S=simple(S)

>> S=double(S) S = 2.08688285305287

Дата добавления: 2014-03-11; просмотров: 468; Нарушение авторских прав

Мы поможем в написании ваших работ!