Энтропия сложного события

Пусть имеются два опыта λ и β.

Опыт λ имеет исходы: x₁, x₂,…,x_m

с вероятностями – p(x₁), p(x₂),…,p(x_m);

а опыт β имеет исходы: y₁, y₂,…,y_k

с вероятностями - p(y₁), p(y₂),…,p(y_k).

В качестве сложного опыта будем рассматривать совместное появление опытов λ и β. Тогда исходами сложного опыта будут (x₁y₁), (x₁y₂),…,(x_my_k);

вероятности этих исходов: p(x₁y₁),…, p(x_iy_j).

Энтропия сложного события:

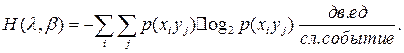
Рассмотрим два случая, когда λ и β независимы и зависимы друг от друга.

1). Опыты λ и β имеют независимые исходы.

Тогда: p(x_iy_j)= p(x_i)·p(y_j).

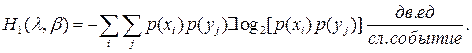
Раскрыв логарифм произведения, получим:

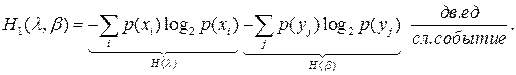
Окончательно получаем: .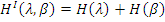

2). Опыты λ и β зависят друг от друга.

Тогда (x_iy_j)= p(x_i)·p(y_j/x_i)

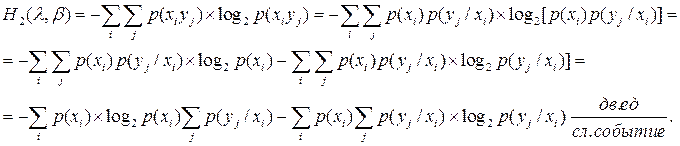
При условии, что произошло событие x_i, имеем:

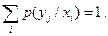
т.к. суммируются вероятности всех событий y_j при условии появления x_i на выходе источника λ.

Выражение

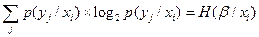
представляет собой энтропию опыта β, при условии, что в опыте λ был исход x_i . Здесь усреднение результатов по опыту β.

Тогда

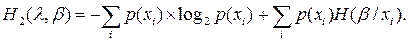
Но первое слагаемое есть H(λ), а второе – условная энтропия H(β/λ), где усреднение уже по опыту λ.

Тогда: 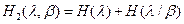, или аналогично .

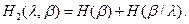Вывод: энтропия сложного события равна сумме энтропий каждого события, если опыты независимы и энтропия равна сумме энтропий одного опыта и условной энтропии другого опыта относительного первого, при двух зависимых опытах (дискретных источниках).

Дата добавления: 2014-03-11; просмотров: 438; Нарушение авторских прав

Мы поможем в написании ваших работ!