
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Первичное кодирование. Теорема Шеннона
Глава II. Передача сообщений по каналам связи без помех
Рассмотрим идеальный канал, где отсутствуют помехи и ошибки. Будем решать задачу кодирования сообщений дискретного источника первичным кодом. Необходимо построить оптимальный первичный код. При этом одним из критериев является избыточность. Т.е., оптимальным будет такой код, у которого избыточность будет минимальной.
Процесс передачи сообщений можно представить в следующем виде:
сообщение→комбинация символов→комбинация сигналов.
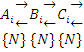
Т.к. помех нет, то все множества сообщений равны.
Преобразование Ai→Bi обеспечивает так называемое первичное кодирующее устройство, а обратное преобразование Bi→Ai – первичное декодирующее устройство. Рассмотрим требования к первичным кодам.
Возьмем:
1) а – основание кода, это есть число символов, используемых для кодирования сообщений. Выбранное основание кода совпадает с основанием системы счисления.
2) n – длина кодовой комбинации, т.е. число символов в самой кодовой комбинации. Например, если двоичная комбинация имеет вид (101110), то n=6.
3) Коды могут быть равномерные (когда все кодовые комбинации имеют одинаковую длину) и неравномерные (длины кодовых комбинаций различны).
Как было сказано выше, оптимальный код должен иметь минимальную избыточность.
Ответ на вопрос о том, какой первичный код можно считать оптимальным, дает первая теорема Шеннона. Рассмотрим трактовку этой торемы применительно к дискретному источнику с множеством сообщений, раным N.
Рассмотрим один случай равновероятных сообщений и другой – появление сообщений на выходе источника с разными вероятностями. Для каждого из этих случаев найдем по первой теореме Шеннона, какой должна быть длина n комбинации оптимального первичного кода.
а) Cобытия A1, A2,…, AN возникают с равными вероятностями p1=p2=…=pN=1/N.
Рассмотрим пример:
Пусть события равновероятные и N=10, pi=0,1; i=1,2…10.
Требуется определить длину комбинации двоичного равномерного первичного кода n.
Найдем H – энтропию дискретного источника: H=log210=3,32 дв.ед./сообщ.
Кодируем сообщение комбинациями одинаковой длины.
В общем виде для построения равномерного первичого кода часто длина комбинации выбирается равной ближайшему большему целому числу в выражении n=[log2N] (верхнее округление). В этом случае для нашего примера имеем n1=[log210]=4.
Имеем следующий вид кодовой комбинации Ai→{a1a2a3a4}.
Такой комбинацией в двоичном виде можно передать 4 дв.ед. информации, а в действительности информационная ёмкость каждого сообщения равна энтропии, т.е. 3,32 дв.ед. Тогда избыточность первичного кода будет 0,68 дв.ед. и, следовательно, такой код не будет оптимальным.
Чтобы добиться более оптимального кода, производим укрупнение событий, т.е. берем сразу по 2 события. Новыми событиямим станут парпы {AiAj} и мы получим новый источник с числом укрупненных сообщений N2 =N²=10² , каждое из которых будет иметь одну и ту же вероятность p(AiAj)=0,01. Закодируем эти укрупненные равновероятные сообщения равномерным первичным кодом с длиной кодовой комбинации n2=[log2N2]=[ log2100]=7 дв.ед/на пару (AiAj).
Тогда на одно исходное сообщение будет приходиться n2=n1/2=3,5 дв.ед./сообщ., т.е., мы получили более оптимальный первичный код.
Для достижения большей оптимальности, т.е. близости к энтропии дискретного источника, произведём дальнейшее укрупнение (по три сообщения).
Получим новый источник равновероятных сообщений (AiAjAz), число которых будет N3=N³=10³. Тогда каждое из этих укрупненных событий можно закодировать двоичным равномерным первичным кодом с длиной комбинации, равной
n3=[log2N3]=[ log210³]=10.
В этом случае на одно исходное сообщение будет приходиться n1=n3/3=3,33 двоичных элемента. При таком укрупнении по 3 исходных сообщений мы получаем практически оптимальный первичный код.
В общем виде алгоритм для определения n оптимального первичного кода по первой теореме Шеннона следующий.
Имеем множество состояний дискретного равновероятного источника N, основание кода – a. Для построения оптимального первичного кода производим укрупнение исходных сообщений по r и получаем как отдельные события (Ai1…Air), количество таких укрупненных равновероятных событий будет равно M=Nr. Закодируем их равномерным первичным кодом с основанием a. При этом получим длину комбинации nr=[logaM]=logaM+∆, где 0<∆<1 – добавка для вернего округления.
Тогда на одно исходное сообщение будет приходиться
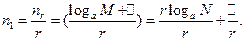 элементов кода с основанием a.
элементов кода с основанием a.
Для получения nопт устремим r к ∞, тогда n1 = nопт=logaN = 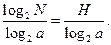
Вывод: для источника с равновероятными исходами первичный код будет оптимальным тогда, когда число элементов на одно сообщение стремится к H/(log2a).
Если код двоичный, то a = 2 и, следоательно, nопт=H.
б) События не равновероятные p1≠p2≠…≠pn. Т.к. события образуют полную группу, то
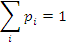
В этом случае предполагаем, что источник содержит N сообщений A1, A2, …, AN, вероятности которых p1 p2 … pN будут различны, т.е. pi≠pj Следовательно, энтропия дискретного источника будет
H=-Σ pi log2 pi
Найдем nопт.
Для этого источник с не равновероятными событиями сводят к источнику с статистически равновероятными событиями. С этой целью события Ai, появляющиеся на выходе дискретного источника, группируют в цепочки событий по S и эти S-цепочки принимают за отдельные сложные события вида (Ai1Ai2…Ais).
Выбираем S достаточно большим, чтобы вероятности появления отдельных S-цепочек были статистически одинаковыми.
Рассмотрим внутреннюю структуру цепочки S. В ней события Ai появляются с вероятностью pi. Определим, сколько раз появится событие Ai в цепочке. В цепочке все события независимы, следовательно Ai появляется в длинной цепочке (piS) раз.
Вероятности цепочек должны быть равны друг другу, т.к. Тогда вероятность произвольной S-цепочки можно считать равной:
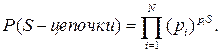
Таким образом, при достаточно большой длине S-цепочек источник с не равновероятными исходными сообщениями преобразуется в источник с равновероятными в среднем укрупненными событиями.
Количество таких укрупненных S-цепочек на выходе преобразованного источника можно принять равным
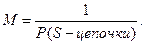
Так как все S-цепочки имеют статистические одинаковые вероятности, то эти равновероятные укрупненные события можно закодировать равномерным первичным кодом. Длина m такой комбинации с основанием кода a будет равна
m= logaM+∆
где 0<∆<1.
Тогда число элементов a-ичного кода, приходящихся на одно исходное сообщение, будет равно:
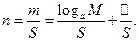
При S → ∞ имеем:
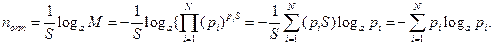
Переходя к двоичному логарифму, получим:
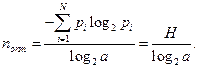
Н – энтропия исходного источника.
Вывод: Для источника с не равновероятными исходами существует такой оптимальный первичный код, у которого средняя длина комбинации сколь угодно близко стремиться к энтропии дискретного источника, деленной на 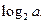
Если код двоичный, то nопт=H.
Рассмотрим это на примере избыточности языка. Предположим, что имеется источник букв русского языка. Число состояний источника N=32. Надо оценитьть:
H0 – энтропию без учета вероятности появления отдельных букв (как если бы все буквы были равновероятны);
H1 – энтропию источника с учетом вероятности появления отдельных букв, при условии независимого их появления.
H2, H3… – энтропию, учитывающую вероятность появления буквосочетаний по две, по три и т.д.
Максимальная из всех энтропия H0, т.к. здесь рассматриваются равновероятностные события.
Вероятность появления сочетаний из нескольких букв меньше, чем появление отдельных букв, поэтому Hi<H1 (i>1).
Минимальной будет энтропия: Hmin=H∞, т.е. энтропия, учитывающая все связи.
Таким образом: H0>H1>H2>…>H∞. H0 и H∞ позволяют оценить избыточность языка. Различают абсолютнуюи относительную избыточность.
Абсолютная избыточность равна разности H0-H∞ или Hmax-Hmin.
Относительная избыточность: (Hmax-Hmin)/ Hmax=η, 0<η<1
Если представить себе язык, у которого η=0, то это был бы такой язык, что появление каждой буквы независимо и равновероятно. Примером такого языка может служить минимальный язык, где появление цифр в последовательности равновероятно.
Язык с η=1 условно можно себе представить как язык, у которого наблюдается полная зависимость, т.е. по одному участку можно восстановить всю последовательность.
Для такого языка H∞→0.
Таблица энтропий для разных языков
| Вероятностные связи | Энтропия на 1 букву [бит] | ||
| Русский текст | английский | немецкий | |
| 1. Вероятностные связи не учитываются (все буквы считаем равновероятными) | Hmax=H0=5 | 4,7 | 4,7 |
| 2. Учитываем вероятность появления отдельных букв | H1=4,34 | 4,4 | 4,1 |
| 3. Учитываем вероятность появления двухбуквенных сочетаний | H2=3,52 | 3,56 | 3,0 |
| 4. Учитываем вероятность появления трехбуквенных сочетаний | H3=3 | 3,3 | 2,6 |
| 5. Учитываем все связи | H∞=1 | 1,6 |
Для русского языка избыточность в среднем равна 5-1=4 бита на букву. Эта избыточность позволяет исправлять ошибки, например, в смысловых текстах и др.
| <== предыдущая страница | | | следующая страница ==> |
| Энтропия сложного события | | | Системы национальных счетов |
Дата добавления: 2014-03-11; просмотров: 698; Нарушение авторских прав

Мы поможем в написании ваших работ!