Холостой ход простейшего трансформатора

В трансформаторах обычного типа поток рассеяния при холостом ходе ничтожно мал (обычно меньше 0,25% от основного потока). Равным образом потери в стали составляют только доли процента от номинальной мощности трансформатора. Поэтому мы сначала изучим режим холостого хода так называемого простейшего трансформатора, т. е. трансформатора без рассеяния и без потерь в меди обмотки и в стали сердечника 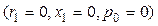. Такой метод предварительного упрощения рассматриваемого вопроса позволяет выделить и изучить сначала сущность процесса или явления, а затем, в случае надобности, внести в него необходимые коррективы.

При анализе работы простейшего трансформатора в режиме холостого хода мы исходим из подводимого к первичной обмотке трансформатора напряжения 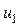и, пользуясь уравнением равновесия первичной обмотки, устанавливаем зависимость между напряжением 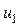и 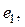создаваемой основным потоком трансформатора; затем устанавливаем зависимость между и основным потоком на основе закона электромагнитной индукции и, наконец, определяем намагничивающий ток 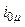, необходимый для создания основного потока, пользуясь законом магнитной цепи.

ЭДС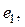. Так как в простейшем трансформаторе 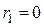и 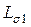=0, то уравнение равновесия первичной обмотки приобретает вид:

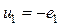(3.1)

т. е. в простейшем трансформаторе подводимое напряжение и наводимое в первичной обмотке находятся в любой момент времени во взаимном равновесии.

В соответствии с существующей эксплуатационной практикой будем считать, что подводимое к трансформатору напряжение 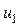является синусоидальной функцией времени. В этом случае

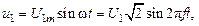(3.2)

где 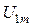– амплитуда подводимого напряжения, 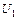– действую-

щее значение его и 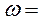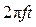– угловая частота.

На рис. 14-2, 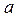напряжение 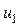и 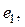показаны кривыми 1 и 2, имеющими одинаковые амплитуды и сдвинутыми друг относительно друга на 180°; следовательно, можно сказать, что кривая 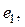является зеркальным отображением кривой 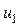относительно оси абсцисс. На этом основании 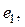часто называют обратной .

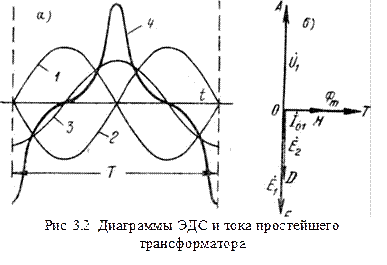
По аналогии с выражением для 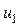имеем:

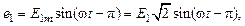(3.3)

На рис. 3.2, б кривые 1 и 2 изображены векторами OA = 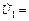– OF = –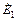для момента времени, когда .

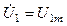Основной магнитный поток 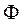. Выразим через поток

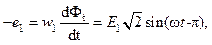
где 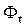– мгновенное значение основного потока.

Интегрируя обе части написанного равенства, имеем:

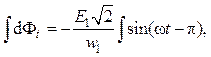
откуда

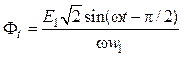, (3.4)

Постоянную интегрирования мы должны принять равной нулю, так как при установившемся режиме работы поток постоянного направления в сердечнике трансформатора отсутствует.

Из формулы (3.4) следует, что при синусоидальном подведенном напряжении магнитный поток простейшего трансформатора представляет собою тоже синусоидальную функцию времени, причем поток опережает первичную на угол 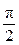, т. е. на четверть периода, или, что одно и то же, первичная отстает от потока на угол 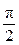(кривая 3 на рис. 3.2, а и вектор ОТ=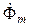на рис. 3.2, б).

Формулу (3.4) можно представить в виде:

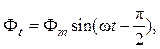(3.5)

где

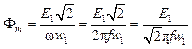(3.6)

амплитуда магнитного потока. Отсюда получается основное в теории трансформатора выражение для действующего значения первичной обмотки:

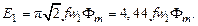(3.7)

Из этой формулы следует, что если частота 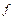и число витков 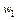заданы, то 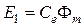, т. е. поток 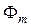прямо пропорционален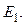Вторичная обмотка пронизывается тем же потоком 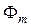. Поэтому действующее значение вторичной обмотки выражается, по аналогии с формулой (3.7), в виде:

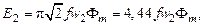(3.8)

где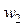– число последовательно соединенных витков вторичной обмотки. По фазе 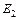так же как и 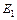отстает от потока 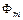на угол 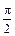(вектор OD на рис. 3.2, б).

Отношение

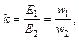(3.9)

так же как раньше отношение 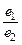, называется коэффициентом трансформации трансформатора или просто коэффициентом трансформации.

Обычно коэффициент трансформации принято определять как отношение большей к меньшей, независимо от того, какая из обмоток является первичной.

Из выражений (3.7) и (3.8) для определяем одну из важнейших величин, характеризующих трансформатор и его свойства, а именно, на виток:

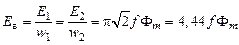(3.10)

В. Намагничивающий ток 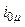. По закону магнитной цепи 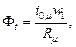где 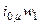– МДС, создаваемая намагничивающим током 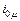; 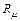– магнитное сопротивление сердечника, состоящее из сопротивления стали и сопротивления в стыках сердечника. Если сталь трансформатора насыщена, как это обычно имеет место в силовых трансформаторах, то форма кривой тока и его амплитуда зависят от степени насыщения стали.

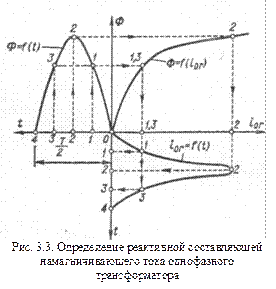
На рис. 3.3 в правом квадранте представлена кривая 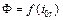при наличии насыщения, а в левом квадранте – синусоидальная кривая 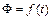, где 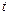– время. В нижнем квадранте этого рисунка изображена кривая 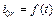, которую можно получить, как показано на рисунке, если значения Ф по кривой 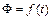для отдельных моментов времени 1, 2, 3 и т. д. снести на кривую 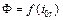и получаемые при этом значения 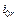снести вниз и отложить для этих же моментов времени. Отрицательная полуволна кривой 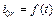будет иметь такую же форму, как и положительная. Такая несинусоидальная кривая 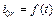(рис. 3.4) содержит все нечетные гармоники (v = 1, 3, 5....), из которых наряду с первой, или основной (v = 1), наиболее сильной будет третья гармоника.

Мы видим, что при синусоидальном потоке кривая тока холостого хода трансформатора с насыщенной сталью несинусоидальна. Мы можем разложить кривую 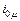в ряд гармонических (рис. 3.4). Так как эта кривая симметрична относительно оси абсцисс, то ряд содержит гармонические только нечетного порядка – первую, третью, пятую и т. д. с амплитудами 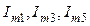и т. д. Первая гармоническая намагничивающего тока совпадает по фазе с основным потоком и, следовательно, отстает от первичного напряжения на 90°. Из числа высших гармонических тока сильнее всего выражена третья. Из последующего изложения мы увидим, что эта гармоническая оказывает значительное влияние на работу трехфазных трансформаторов при некоторых способах соединения их обмоток. Гармонические высших порядков выражены слабее, чем третья, и поэтому их влиянием чаще всего пренебрегают.

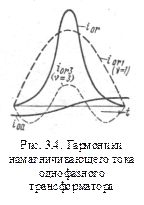
Процентное содержание высших гармонических в кривой тока холостого хода тем больше, чем выше амплитуда индукции.

Зная амплитуды гармонических в кривой тока холостого хода, мы можем определить действующее значение этого тока по общеизвестной формуле:

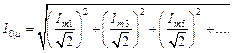(3.11)

Так как ток холостого хода несинусоидален, то на векторной диаграмме может быть показана только первая гармоническая этого тока 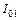(рис. 3.2, б), поскольку на векторных диаграммах могут изображаться величины только какой-нибудь одной периодичности. Таким образом, диаграмма холостого хода носит в отношении тока холостого хода приближенный характер, что необходимо иметь в виду как здесь, так и при построении диаграмм в дальнейшем. Но при практических приближенных построениях обычно исходят из эквивалентного синусоидального тока холостого хода, имеющего действующее значение 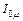(формула 3.11.)

Так как ток 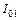отстает от напряжения 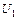на 90°, то активная мощность этой гармонической равна нулю; мощности высших гармонических также равны нулю, поскольку они имеют периодичность, отличную от периодичности напряжения. Следовательно, активная мощность, потребляемая простейшим трансформатором из сети, равна нулю, чего и следовало ждать, так как, согласно условию, в простейшем трансформаторе потери приняты равными нулю.

Дата добавления: 2014-03-11; просмотров: 455; Нарушение авторских прав

Мы поможем в написании ваших работ!