
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Математическое отступление
.
В правой части равенства слагаемые имеют следующий физический смысл:
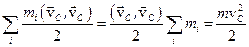 - кинетическая энергия центра масс системы;
- кинетическая энергия центра масс системы;
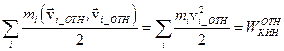 - кинетическая энергия относительного движения точек;
- кинетическая энергия относительного движения точек;
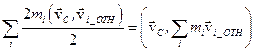 , но
, но 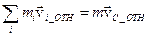 , где
, где 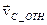 - относительная скорость центра масс в системе отсчета, где центр масс покоится. Очевидно, что
- относительная скорость центра масс в системе отсчета, где центр масс покоится. Очевидно, что 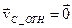 , поэтому для этого слагаемого получаем:
, поэтому для этого слагаемого получаем:
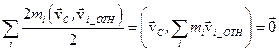 .
.
Окончательно исходное равенство примет вид:

Полная кинетическая энергия тела (системы точек) равна сумме кинетической энергии той же системы в её движении относительно системы центра масс и кинетической энергии, которую имела бы рассматриваемая систем, двигаясь поступательно со скоростью её центра масс.
Это утверждение принято называть теоремой Кёнига. Из теоремы Кёнига следует, что кинетическая энергия твёрдого тела равна сумме его кинетической энергии в поступательном движении со скоростью центра масс тела и кинетической энергии вращения этого тела вокруг центра масс.
Пример. Определить кинетическую энергию диска массой m и радиуса R, катящегося без проскальзывания со скоростью 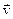 .
.
Решение. Так как диск катится без проскальзывания, то скорость центра масс равна 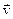 и величина скорости вращения точек края диска относительно оси, проходящей через центр масс и перпендикулярной плоскости диска, тоже равна v. Следовательно, полная кинетическая энергия:
и величина скорости вращения точек края диска относительно оси, проходящей через центр масс и перпендикулярной плоскости диска, тоже равна v. Следовательно, полная кинетическая энергия:
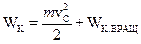 .
.
При вращении диска вокруг центра масс угловая скорость всех точек равна 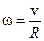 , поэтому кинетическая энергия вращения
, поэтому кинетическая энергия вращения 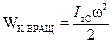 . Момент инерции диска относительно рассматриваемой оси вращения равен
. Момент инерции диска относительно рассматриваемой оси вращения равен 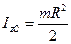 . Тогда кинетическая энергия в поступательном движении со скоростью центра масс диска равна
. Тогда кинетическая энергия в поступательном движении со скоростью центра масс диска равна  . Следовательно
. Следовательно 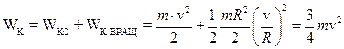 .§
.§
Пусть задана функция от нескольких аргументов, являющаяся непрерывно-дифференцируемой по каждому из них: 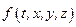 . Производная такой функции по одному из аргументов (например, по x) при условии, что остальные не меняются, называется частной производной по данному аргументу и обозначается
. Производная такой функции по одному из аргументов (например, по x) при условии, что остальные не меняются, называется частной производной по данному аргументу и обозначается 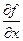 .
.
Пусть в трёхмерном пространстве задана непрерывно дифференцируемая функция 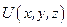 . Рассмотрим значения этой функции в двух соседних точках пространства, отстоящих друг от друга на малый вектор
. Рассмотрим значения этой функции в двух соседних точках пространства, отстоящих друг от друга на малый вектор 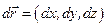 :
:
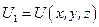 и
и 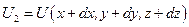 .
.
Тогда разложение в ряд Тейлора для функции U вблизи точки 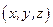 имеет вид:
имеет вид:
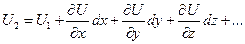
Если ввести вектор 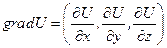 , который называется градиентом функции U, и отбросить остальные слагаемые в разложении (которые обозначены точками), то для приращения функции U можно записать:
, который называется градиентом функции U, и отбросить остальные слагаемые в разложении (которые обозначены точками), то для приращения функции U можно записать:
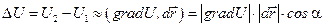 ,
,
где a - угол между векторами 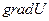 и
и 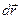 .
.
| <== предыдущая страница | | | следующая страница ==> |
| КИНЕТИЧЕСКАЯ ЭНЕРГИЯ ТЕЛА (СИСТЕМЫ ТОЧЕК) | | | Свойства градиента функции |
Дата добавления: 2014-03-11; просмотров: 413; Нарушение авторских прав

Мы поможем в написании ваших работ!